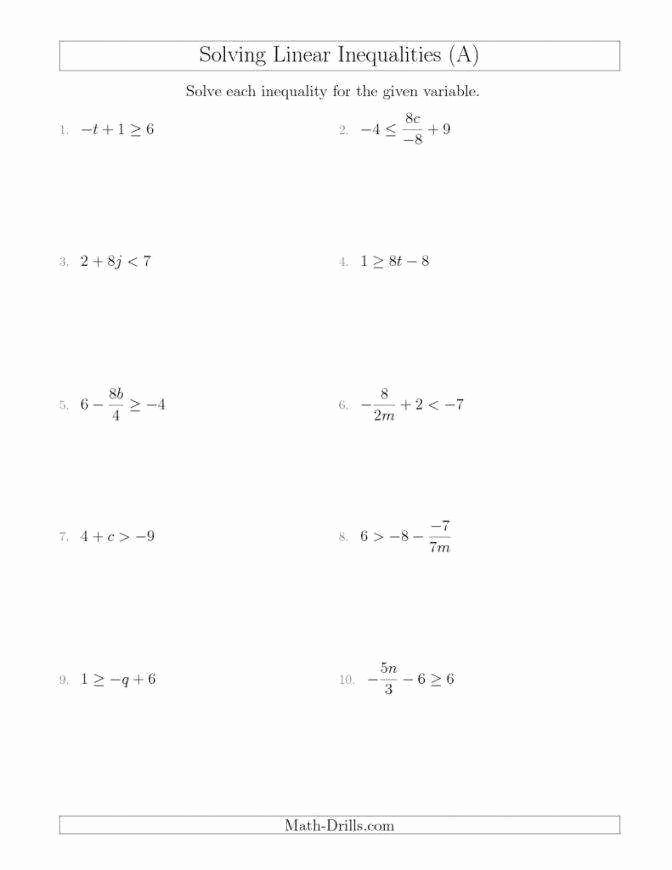Graphing Linear Inequalities Worksheet Answers Made Easy
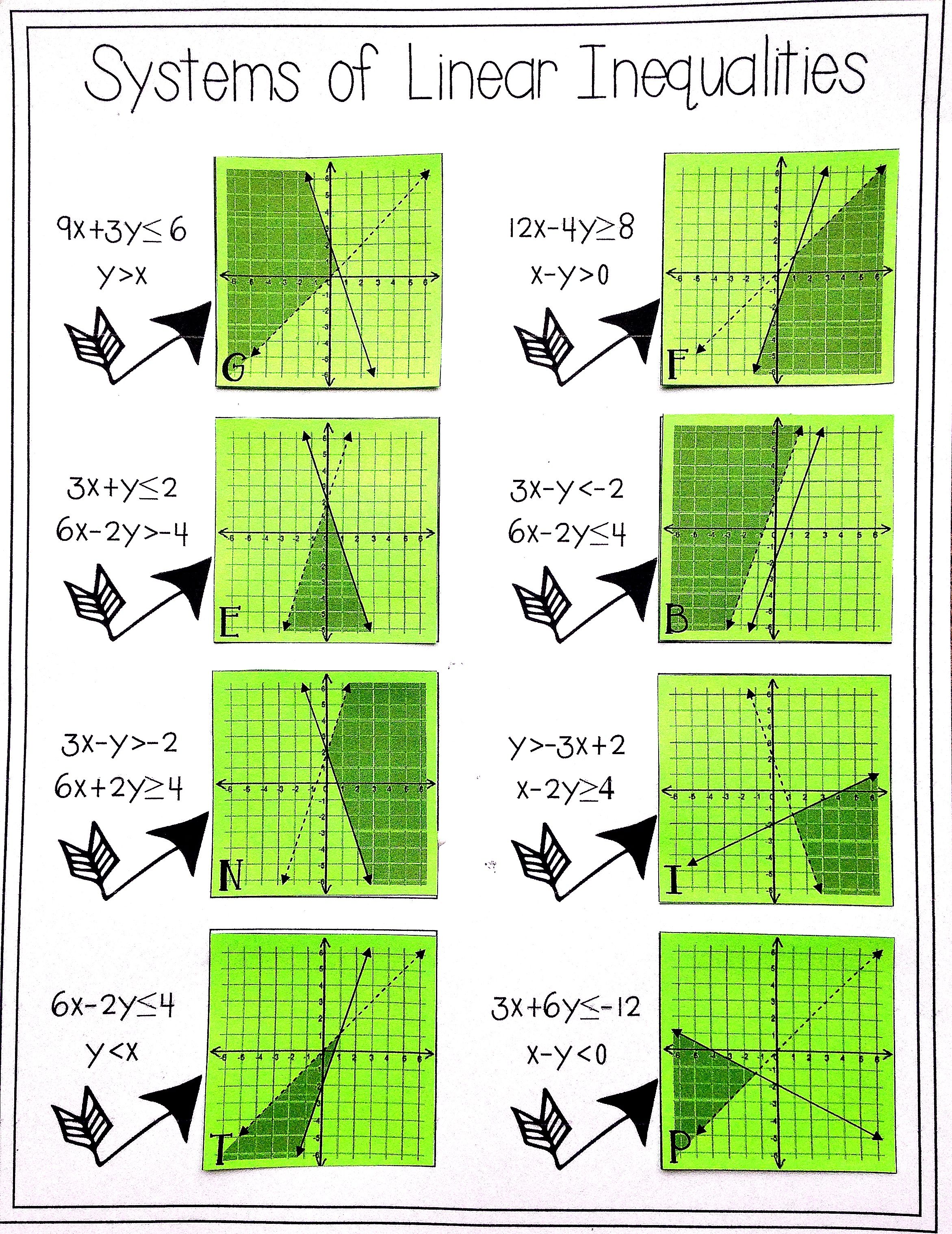
Understanding Linear Inequalities and How to Graph Them
Graphing linear inequalities is a fundamental concept in algebra and mathematics. It involves representing the solution to an inequality on a coordinate plane. In this blog post, we will delve into the world of linear inequalities, understand the different types, and learn how to graph them with ease.
What are Linear Inequalities?
A linear inequality is a statement that two expressions are not equal. It is represented by the symbols <, >, ≤, or ≥. The solution to a linear inequality is a set of values that make the inequality true. Linear inequalities can be represented in one variable or two variables.
Types of Linear Inequalities
There are several types of linear inequalities, including:
- Simple Linear Inequality: A simple linear inequality involves only one variable. For example, 2x + 3 > 5.
- Compound Linear Inequality: A compound linear inequality involves two or more simple linear inequalities joined by a logical operator. For example, 2x + 3 > 5 and x - 2 < 3.
- Linear Inequality in Two Variables: A linear inequality in two variables involves two variables. For example, 2x + 3y > 5.
How to Graph Linear Inequalities
Graphing linear inequalities involves representing the solution to the inequality on a coordinate plane. Here are the steps to graph a linear inequality:
- Write the inequality in slope-intercept form: Rewrite the inequality in slope-intercept form (y = mx + b), where m is the slope and b is the y-intercept.
- Graph the boundary line: Graph the boundary line by plotting two points and drawing a line through them. The boundary line should be a solid line for ≤ or ≥ inequalities and a dashed line for < or > inequalities.
- Shade the region: Shade the region above or below the boundary line, depending on the inequality. For example, if the inequality is y > 2x + 3, shade the region above the boundary line.
💡 Note: When graphing a linear inequality, make sure to shade the correct region. If the inequality is ≤ or ≥, shade the region that includes the boundary line. If the inequality is < or >, shade the region that does not include the boundary line.
Examples of Graphing Linear Inequalities
Here are some examples of graphing linear inequalities:
- Example 1: Graph the inequality 2x + 3y > 5.
Solution: Rewrite the inequality in slope-intercept form (y = -2/3x + 5⁄3). Graph the boundary line by plotting two points and drawing a dashed line through them. Shade the region above the boundary line.
- Example 2: Graph the inequality x - 2y ≤ 3.
Solution: Rewrite the inequality in slope-intercept form (y = 1/2x - 3⁄2). Graph the boundary line by plotting two points and drawing a solid line through them. Shade the region below the boundary line.
Graphing Linear Inequalities Worksheet Answers
Here are the answers to some common graphing linear inequalities worksheet problems:

| Inequality | Graph |
|---|---|
| 2x + 3y > 5 | Shade the region above the boundary line |
| x - 2y ≤ 3 | Shade the region below the boundary line |
| y > 2x + 3 | Shade the region above the boundary line |
| x + 2y ≥ 4 | Shade the region below the boundary line |
📝 Note: These are just some examples of graphing linear inequalities. Make sure to practice graphing different types of linear inequalities to become proficient.
Graphing linear inequalities is a fundamental concept in algebra and mathematics. By following the steps outlined in this blog post, you can easily graph linear inequalities and become proficient in solving them.
Summarizing the key points, graphing linear inequalities involves representing the solution to the inequality on a coordinate plane. The steps to graph a linear inequality include writing the inequality in slope-intercept form, graphing the boundary line, and shading the region. By practicing graphing different types of linear inequalities, you can become proficient in solving them.
What is a linear inequality?
+A linear inequality is a statement that two expressions are not equal. It is represented by the symbols <, >, ≤, or ≥.
How do you graph a linear inequality?
+To graph a linear inequality, write the inequality in slope-intercept form, graph the boundary line, and shade the region.
What is the difference between a simple linear inequality and a compound linear inequality?
+A simple linear inequality involves only one variable, while a compound linear inequality involves two or more simple linear inequalities joined by a logical operator.
Related Terms:
- Graphing Linear Inequalities Worksheet PDF
- Graphing Linear Inequalities Kuta
- Systems of linear inequalities worksheet
- Linear Inequalities answer key