Mastering Fractions in 5 Easy Steps for Grade 5

Mastering Fractions in 5 Easy Steps for Grade 5
Learning fractions can be a challenging but exciting experience for grade 5 students. Fractions are a fundamental concept in mathematics, and understanding them can open doors to more advanced math topics. In this article, we will break down the process of mastering fractions into 5 easy steps that are perfect for grade 5 students.
Step 1: Understanding the Concept of Fractions
Before diving into the nitty-gritty of fractions, it’s essential to understand what they represent. A fraction is a way to show part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator tells us how many equal parts we have, and the denominator tells us how many parts the whole is divided into.
For example, in the fraction 3⁄4, the numerator is 3, and the denominator is 4. This means we have 3 equal parts out of a total of 4 parts.
Step 2: Visualizing Fractions
Visualizing fractions is crucial to understanding them better. You can use real-life objects, diagrams, or pictures to represent fractions. For instance, you can draw a pizza that is divided into 8 slices, and 3 of them are shaded to represent the fraction 3⁄8.
📝 Note: Use everyday objects to make fractions more relatable and fun for grade 5 students.
Here’s a simple table to illustrate some common fractions with visual representations:
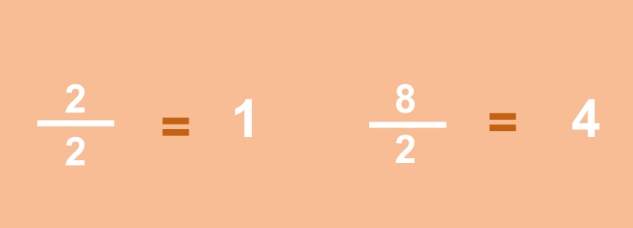
| Fraction | Visual Representation |
|---|---|
| 1/2 | A cake divided into 2 equal parts, with 1 part shaded |
| 3/4 | A pizza divided into 4 equal parts, with 3 parts shaded |
| 2/3 | A rectangle divided into 3 equal parts, with 2 parts shaded |
Step 3: Simplifying Fractions
Simplifying fractions is an essential skill to master. To simplify a fraction, we need to find the greatest common divisor (GCD) of the numerator and the denominator and divide both numbers by the GCD.
For example, to simplify the fraction 6⁄8, we need to find the GCD of 6 and 8, which is 2. Then, we divide both numbers by 2 to get the simplified fraction 3⁄4.
📝 Note: Use online tools or calculators to find the GCD and simplify fractions quickly.
Step 4: Adding and Subtracting Fractions
Adding and subtracting fractions can be a bit tricky, but it’s easy once you understand the concept. To add or subtract fractions, we need to have the same denominator. If the denominators are different, we need to find the least common multiple (LCM) of the two denominators.
For example, to add the fractions 1⁄4 and 1⁄6, we need to find the LCM of 4 and 6, which is 12. Then, we convert both fractions to have a denominator of 12:
- 1⁄4 = 3⁄12
- 1⁄6 = 2⁄12
Now, we can add the fractions:
- 3⁄12 + 2⁄12 = 5⁄12
Step 5: Real-World Applications of Fractions
Fractions are all around us, and understanding them can help us in real-life situations. Here are a few examples:
- Cooking: Recipes often involve fractions, such as 1⁄4 cup of flour or 3⁄4 teaspoon of salt.
- Shopping: Prices and discounts often involve fractions, such as 1⁄2 off or 3⁄4 of the original price.
- Sports: Statistics in sports, such as baseball or basketball, often involve fractions, such as a batting average of 3⁄4 or a free-throw percentage of 2⁄3.
By mastering fractions, grade 5 students can develop a deeper understanding of the world around them and build a strong foundation for more advanced math concepts.
Summing Up
Mastering fractions in 5 easy steps is a great way for grade 5 students to build a strong foundation in mathematics. By understanding the concept of fractions, visualizing them, simplifying them, adding and subtracting them, and applying them to real-world situations, students can become confident and proficient in their math skills. With practice and patience, mastering fractions can be a fun and rewarding experience for grade 5 students.
What is a fraction?
+A fraction is a way to show part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number).
How do I simplify a fraction?
+To simplify a fraction, find the greatest common divisor (GCD) of the numerator and the denominator and divide both numbers by the GCD.
How do I add fractions with different denominators?
+To add fractions with different denominators, find the least common multiple (LCM) of the two denominators and convert both fractions to have the same denominator.
Related Terms:
- Multiplying Fractions worksheet pdf
- Dividing fractions Worksheet PDF
- Fraction addition and subtraction worksheet
- Fraction Worksheet Grade 4