Geometry Trig Word Problems Made Easy

Unlocking the Secrets of Geometry Trig Word Problems

Geometry trig word problems can be daunting, but with the right approach, they can be made easy. In this comprehensive guide, we’ll break down the steps to solve these problems and provide you with the tools you need to become a master problem-solver.

Understanding the Basics

Before we dive into the nitty-gritty of solving geometry trig word problems, let’s review the basics. Geometry trig involves the use of trigonometric functions to solve problems involving right triangles. The key trig functions you need to know are:

• Sine (sin): The ratio of the opposite side to the hypotenuse.
• Cosine (cos): The ratio of the adjacent side to the hypotenuse.
• Tangent (tan): The ratio of the opposite side to the adjacent side.

These functions can be used to solve problems involving right triangles, which are triangles with one right angle (90 degrees).

Step-by-Step Guide to Solving Geometry Trig Word Problems

Now that we’ve covered the basics, let’s move on to the step-by-step guide to solving geometry trig word problems.

Step 1: Read the Problem Carefully

Read the problem carefully and identify the key elements:

• Given information: What information is provided in the problem?
• Unknown quantities: What quantities are you trying to find?
• Overall objective: What is the problem asking you to do?

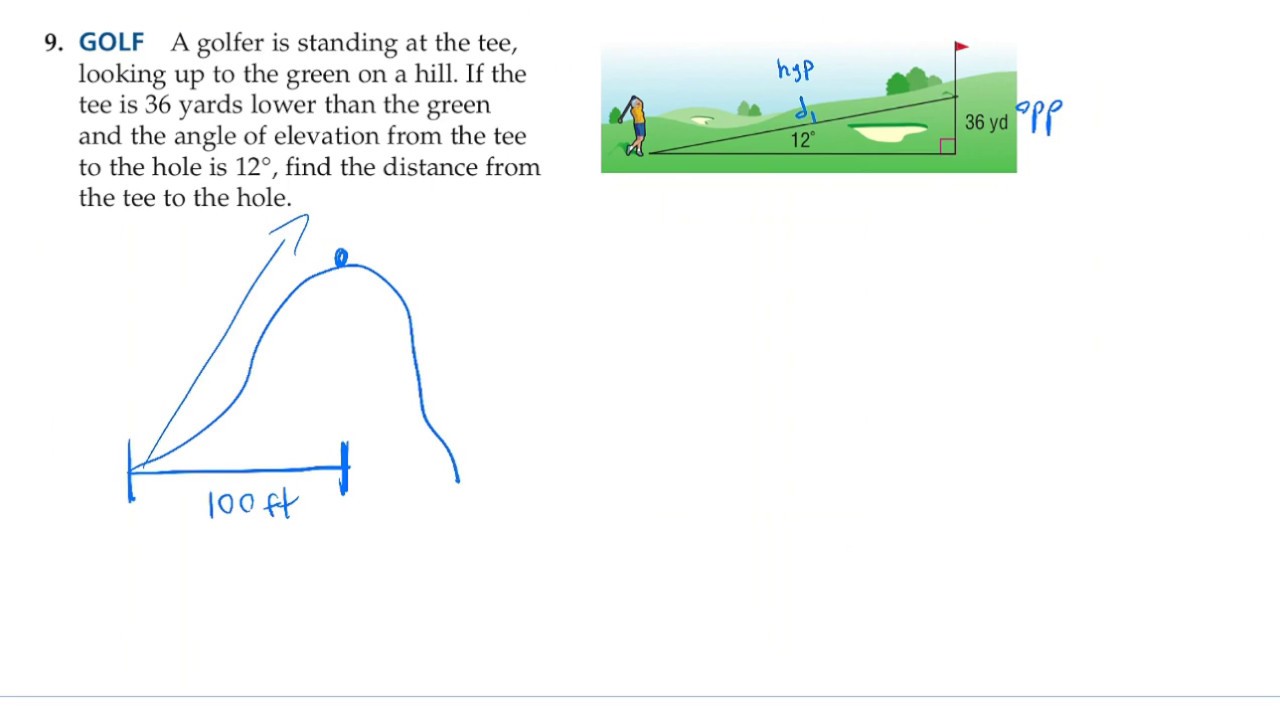
Step 2: Draw a Diagram

Draw a diagram to visualize the problem. This will help you to:

• Identify the right triangle: Locate the right triangle in the diagram.
• Label the sides: Label the sides of the triangle with the given information.
• Determine the trig function: Determine which trig function to use based on the given information and the unknown quantities.

Step 3: Choose the Correct Trig Function

Choose the correct trig function based on the given information and the unknown quantities:

• SOH-CAH-TOA: Use the SOH-CAH-TOA mnemonic to remember the trig functions:
  • Sine = Opposite side / Hypotenuse
  • Cosine = Adjacent side / Hypotenuse
  • Tangent = Opposite side / Adjacent side

Step 4: Plug in the Values

Plug in the values into the chosen trig function:

• Make sure the values are in the correct units: Ensure that the values are in the correct units, such as degrees or radians.
• Simplify the expression: Simplify the expression to get the final answer.

Step 5: Check the Answer

Check the answer to ensure that it makes sense:

• Check the units: Check that the answer is in the correct units.
• Check the reasonableness: Check that the answer is reasonable based on the context of the problem.

Examples of Geometry Trig Word Problems

Let’s look at some examples of geometry trig word problems:

Example 1

A building is 50 meters tall. If the angle of elevation to the top of the building is 30 degrees, how far is the building from the point of observation?

• Given information: Height of the building = 50 meters, Angle of elevation = 30 degrees
• Unknown quantity: Distance from the point of observation to the building
• Trig function: Tangent (tan)

Using the tangent function, we get:

tan(30) = 50 / x

x = 50 / tan(30)

x ≈ 86.6 meters

Example 2

A ship is sailing towards a lighthouse. The angle of depression from the top of the lighthouse to the ship is 45 degrees. If the height of the lighthouse is 100 meters, how far is the ship from the lighthouse?

• Given information: Height of the lighthouse = 100 meters, Angle of depression = 45 degrees
• Unknown quantity: Distance from the ship to the lighthouse
• Trig function: Cosine (cos)

Using the cosine function, we get:

cos(45) = 100 / x

x = 100 / cos(45)

x ≈ 141.4 meters

Common Mistakes to Avoid

When solving geometry trig word problems, there are several common mistakes to avoid:

• Not reading the problem carefully: Failing to read the problem carefully can lead to misunderstandings and incorrect solutions.
• Not drawing a diagram: Failing to draw a diagram can make it difficult to visualize the problem and identify the right triangle.
• Using the wrong trig function: Using the wrong trig function can lead to incorrect solutions.

🚨 Note: Always check your units and reasonableness of your answer to ensure that it makes sense in the context of the problem.

Now that we’ve covered the basics and provided a step-by-step guide to solving geometry trig word problems, you’re ready to tackle these problems with confidence. Remember to read the problem carefully, draw a diagram, choose the correct trig function, plug in the values, and check your answer.

Without the proper tools and techniques, geometry trig word problems can be overwhelming. But with the right approach, they can be made easy. With practice and patience, you’ll become a master problem-solver and be able to tackle even the most challenging geometry trig word problems.

Related Terms:

• Trigonometry Word Problems worksheets pdf
• Trig word problems hard