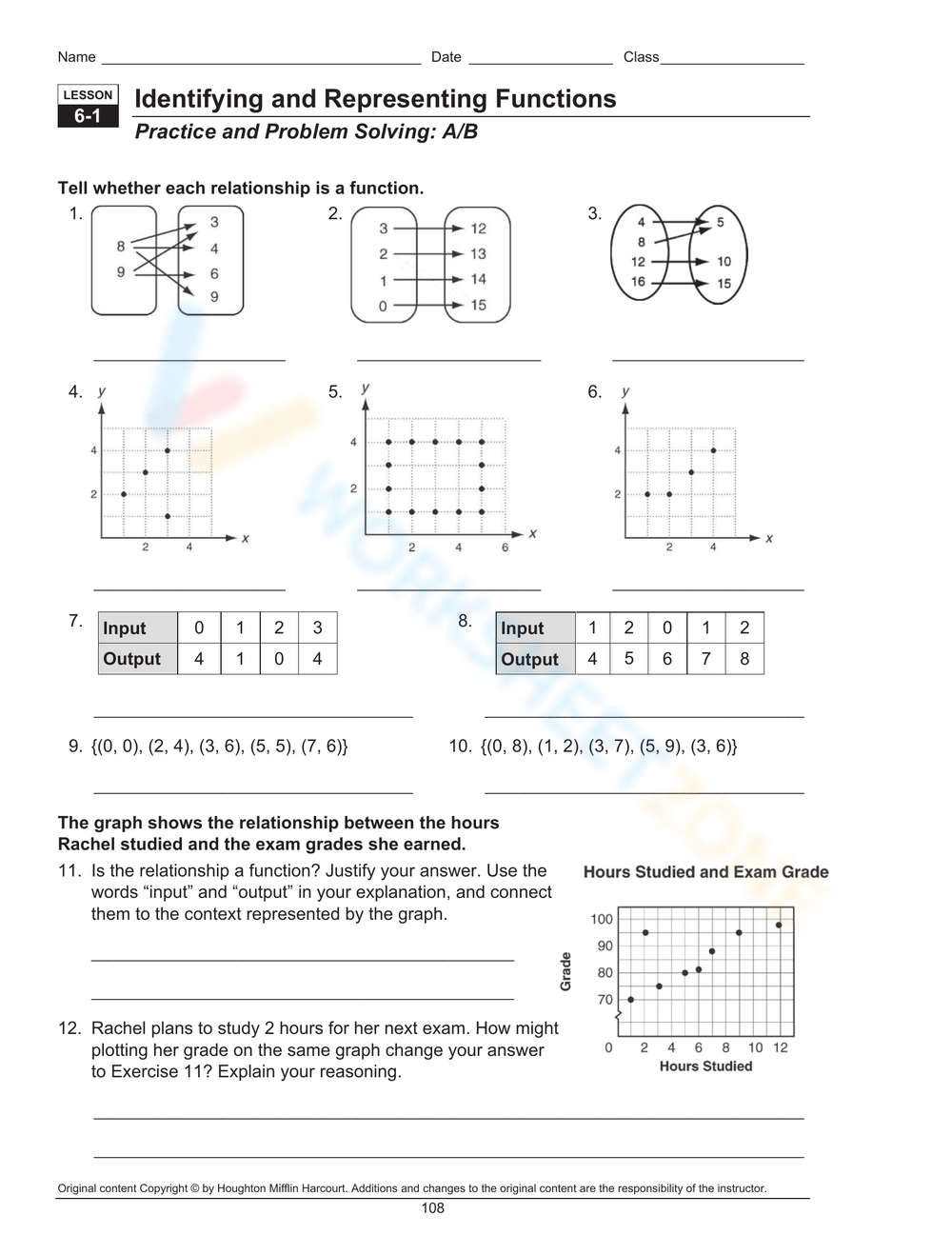
Functions Mapping Worksheet Answer Key

Understanding Functions and Mapping
Functions are a fundamental concept in mathematics, and mapping is a crucial aspect of understanding how functions work. In this answer key, we will delve into the world of functions and explore how mapping can help us visualize and analyze functions.
What is a Function?
A function is a relation between a set of inputs, called the domain, and a set of possible outputs, called the range. It is a way of describing a relationship between variables, where each input corresponds to exactly one output.
What is Mapping?
Mapping is a way of visualizing functions by representing the input-output pairs as a diagram. It is a powerful tool for understanding how functions work and for identifying patterns and relationships between variables.
Types of Functions
There are several types of functions, including:
- Linear Functions: These are functions that can be represented by a straight line. They have a constant rate of change and can be written in the form f(x) = mx + b.
- Quadratic Functions: These are functions that can be represented by a parabola. They have a rate of change that is not constant and can be written in the form f(x) = ax^2 + bx + c.
- Exponential Functions: These are functions that involve a variable base and a constant exponent. They can be written in the form f(x) = ab^x.
Mapping Functions
When mapping a function, we use a diagram to show the relationship between the input and output values. The diagram consists of a set of input values, called the domain, and a set of output values, called the range.
Here is an example of a mapping diagram for a simple linear function:
| Input (x) | Output (f(x)) |
|---|---|
| 0 | 2 |
| 1 | 4 |
| 2 | 6 |
| 3 | 8 |
Analyzing Functions using Mapping
By analyzing a mapping diagram, we can gain insight into the behavior of a function. We can identify patterns and relationships between the input and output values, and we can use this information to make predictions about the function’s behavior.
Example: Analyzing a Linear Function
Suppose we have a linear function f(x) = 2x + 1, and we want to analyze its behavior using mapping.
| Input (x) | Output (f(x)) |
|---|---|
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
From this mapping diagram, we can see that the function has a constant rate of change of 2. This means that for every increase of 1 in the input value, the output value increases by 2.
Example: Analyzing a Quadratic Function
Suppose we have a quadratic function f(x) = x^2 + 2x + 1, and we want to analyze its behavior using mapping.
| Input (x) | Output (f(x)) |
|---|---|
| -2 | 1 |
| -1 | 0 |
| 0 | 1 |
| 1 | 4 |
| 2 | 9 |
From this mapping diagram, we can see that the function has a rate of change that is not constant. The output values increase rapidly as the input values increase.
Conclusion
In conclusion, mapping is a powerful tool for understanding and analyzing functions. By using a diagram to visualize the input-output pairs, we can gain insight into the behavior of a function and make predictions about its behavior. Whether we are working with linear, quadratic, or exponential functions, mapping can help us understand the relationships between variables and make informed decisions.
FAQ Section
What is the difference between a function and a relation?
+A function is a relation between a set of inputs and a set of possible outputs, where each input corresponds to exactly one output. A relation, on the other hand, is a more general term that refers to any connection between two sets of values.
What is the purpose of mapping in functions?
+The purpose of mapping in functions is to visualize the input-output pairs and gain insight into the behavior of the function. It helps us identify patterns and relationships between variables and make predictions about the function’s behavior.
What are the different types of functions?
+There are several types of functions, including linear functions, quadratic functions, and exponential functions. Each type of function has its own unique characteristics and behaviors.
Related Terms:
- Identifying and Representing Functions worksheet
- Functions table worksheet answer key
- Functions ordered pairs worksheet
- Identifying Functions Worksheet pdf
- Function mapping worksheet
- Functions Substitution worksheet



