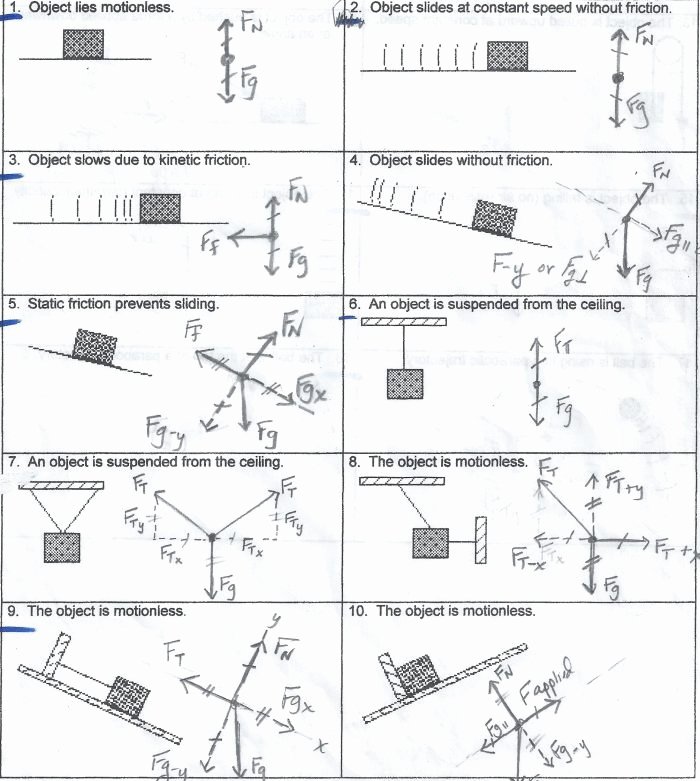
Free-Body Diagram Worksheet Answers & Solutions

Understanding Free-Body Diagrams: A Comprehensive Guide

Free-body diagrams are a fundamental tool in physics and engineering, used to visualize and analyze the forces acting on an object. They help us to simplify complex problems, identify the forces involved, and solve for unknowns. In this article, we will explore the concept of free-body diagrams, their importance, and provide a step-by-step guide on how to draw and solve them.

What is a Free-Body Diagram?

A free-body diagram is a graphical representation of an object, showing all the forces acting on it. It is a simplified diagram that isolates the object from its surroundings, allowing us to focus on the forces that affect its motion. Free-body diagrams are essential in solving problems involving Newton’s laws of motion, particularly the second law, which relates the net force acting on an object to its resulting acceleration.

Why are Free-Body Diagrams Important?

Free-body diagrams are important for several reasons:

• Simplifies complex problems: By isolating the object and showing only the forces acting on it, free-body diagrams help to break down complex problems into manageable parts.
• Helps to identify forces: Free-body diagrams enable us to identify all the forces acting on an object, including external forces like gravity, friction, and normal forces.
• Essential for solving problems: Free-body diagrams are necessary for solving problems involving Newton’s laws of motion, particularly the second law.

How to Draw a Free-Body Diagram

Drawing a free-body diagram is a straightforward process. Here’s a step-by-step guide:

1. Isolate the object: Start by isolating the object from its surroundings. Draw a simple shape to represent the object, such as a box or a circle.
2. Identify the forces: Identify all the forces acting on the object, including:
   • Gravity (weight)
   • Friction (kinetic or static)
   • Normal forces (perpendicular to the surface)
   • Tension (in strings or ropes)
   • Applied forces (pushes or pulls)
3. Draw the forces: Draw each force as an arrow, labeled with its magnitude (if known) and direction. Use a key or legend to distinguish between different types of forces.
4. Include angles: Include any relevant angles between forces or between forces and the object’s motion.

Solving Free-Body Diagrams

Once you have drawn a free-body diagram, you can use it to solve problems involving Newton’s laws of motion. Here’s a step-by-step guide:

1. Sum the forces: Sum all the forces acting on the object in the x- and y-directions. Use the following equations:
   • ΣF_x = m * a_x
   • ΣF_y = m * a_y
2. Apply Newton’s second law: Use Newton’s second law to relate the net force to the object’s resulting acceleration.
3. Solve for unknowns: Solve for any unknowns, such as the magnitude of a force or the object’s acceleration.

Example Problem: Free-Body Diagram Worksheet

A block of mass 5 kg is pulled up a frictionless incline by a force of 20 N. The angle of the incline is 30°. Draw a free-body diagram and find the acceleration of the block.

Solution

1. Isolate the object: Draw a simple shape to represent the block.

2. Identify the forces:

• Gravity (weight)
• Normal force (perpendicular to the incline)
• Applied force (20 N)

1. Draw the forces: Draw each force as an arrow, labeled with its magnitude and direction.

2. Sum the forces: ΣF_x = F_app - F_g * sin(30°) = m * a_x ΣF_y = F_N - F_g * cos(30°) = 0 (since the block is not moving perpendicular to the incline)

3. Apply Newton’s second law: F_app - F_g * sin(30°) = m * a_x

4. Solve for unknowns: a_x = (F_app - F_g * sin(30°)) / m

Answers and Solutions

Problem	Free-Body Diagram	Solution
A block of mass 5 kg is pulled up a frictionless incline by a force of 20 N. The angle of the incline is 30°.		a_x = (20 N - 5 kg \* 9.8 m/s^2 \* sin(30°)) / 5 kg = 2.6 m/s^2
A car of mass 1500 kg is moving along a horizontal road with a constant velocity of 25 m/s. The coefficient of friction between the tires and the road is 0.8.		F_f = μ \* F_N = 0.8 \* 1500 kg \* 9.8 m/s^2 = 11760 N
A rope is pulling a box of mass 10 kg up a frictionless incline at a constant speed. The angle of the incline is 45°. If the tension in the rope is 50 N, what is the weight of the box?		F_g = F_T / cos(45°) = 50 N / 0.707 = 70.7 N

Notes

💡 Note: When drawing free-body diagrams, make sure to include all the forces acting on the object, even if they are not explicitly mentioned in the problem.

📝 Note: Use a key or legend to distinguish between different types of forces in your free-body diagram.

Conclusion

Free-body diagrams are a powerful tool for solving problems involving Newton’s laws of motion. By following the steps outlined in this article, you can draw and solve free-body diagrams with confidence. Remember to include all the forces acting on the object, and use Newton’s second law to relate the net force to the object’s resulting acceleration.

FAQ