Fractions Greater Than 1 Made Easy with Practice
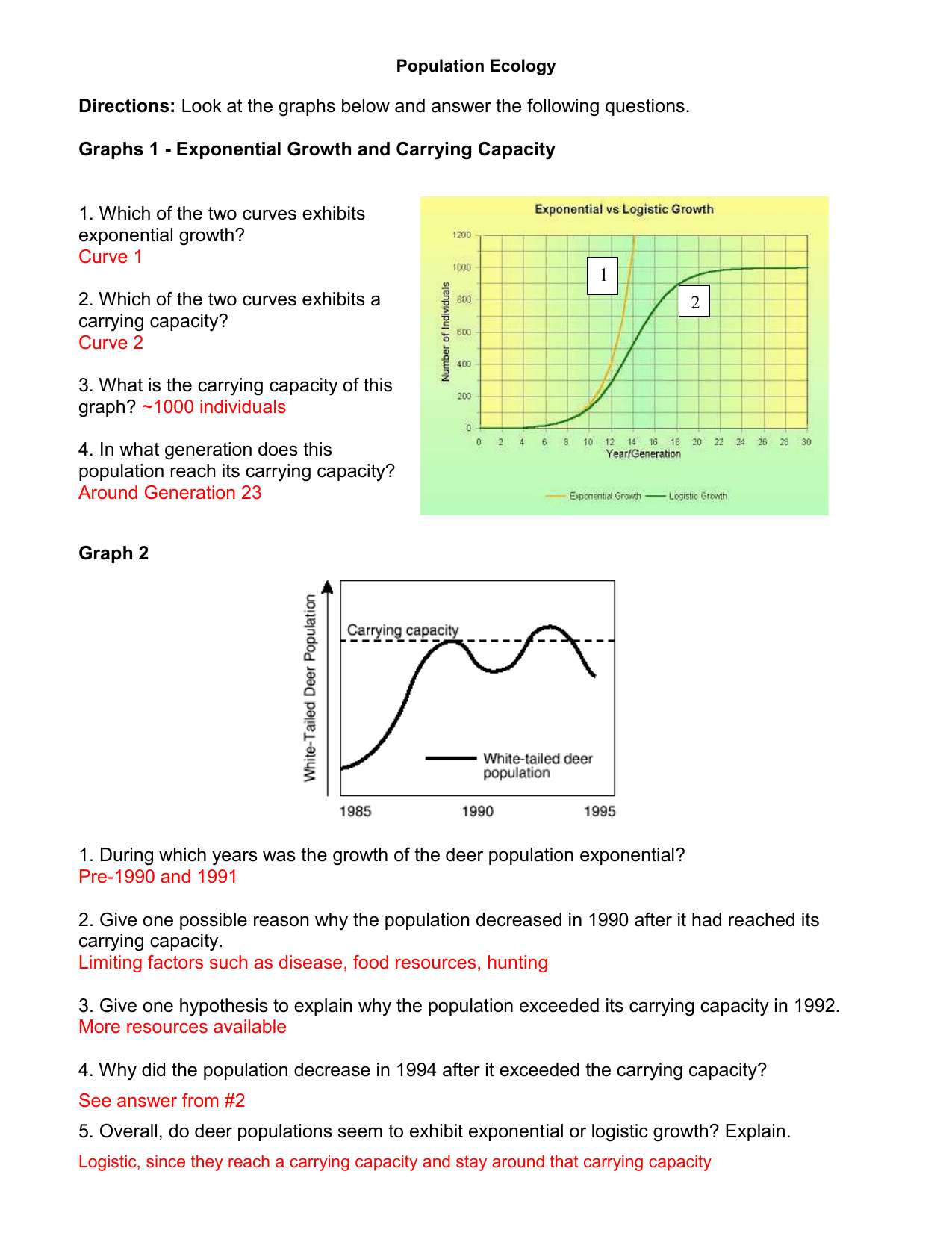
Understanding Fractions Greater Than 1
Fractions are a fundamental concept in mathematics, and understanding them is crucial for various mathematical operations. While fractions less than 1 are relatively easy to comprehend, fractions greater than 1 can be a bit more challenging. In this article, we will explore fractions greater than 1, their representation, and provide practice exercises to help you master this concept.
What are Fractions Greater Than 1?
Fractions greater than 1, also known as improper fractions, are fractions where the numerator is greater than the denominator. For example, 3⁄2, 5⁄3, and 7⁄4 are all improper fractions. These fractions can be converted to mixed numbers, which consist of a whole number and a proper fraction.
Converting Improper Fractions to Mixed Numbers
Converting improper fractions to mixed numbers is a straightforward process. To do this, you need to divide the numerator by the denominator and write the remainder as a fraction. For instance, let’s convert the improper fraction 5⁄3 to a mixed number:
Step 1: Divide the numerator (5) by the denominator (3): 5 ÷ 3 = 1 with a remainder of 2.
Step 2: Write the result as a mixed number: 1 2⁄3.
📝 Note: When converting improper fractions to mixed numbers, the whole number part is the quotient, and the fraction part is the remainder divided by the denominator.
Adding and Subtracting Fractions Greater Than 1
Adding and subtracting fractions greater than 1 is similar to adding and subtracting proper fractions. However, you need to follow some rules:
Adding Fractions: To add fractions greater than 1, follow these steps:
- Find the least common multiple (LCM) of the denominators.
- Convert both fractions to have the LCM as the denominator.
- Add the numerators.
- Simplify the result.
Subtracting Fractions: To subtract fractions greater than 1, follow these steps:
- Find the LCM of the denominators.
- Convert both fractions to have the LCM as the denominator.
- Subtract the numerators.
- Simplify the result.
Example: Add 3⁄2 and 2⁄3.
Step 1: Find the LCM of 2 and 3, which is 6.
Step 2: Convert both fractions to have a denominator of 6: 3⁄2 = 9⁄6 and 2⁄3 = 4⁄6.
Step 3: Add the numerators: 9 + 4 = 13.
Step 4: Simplify the result: 13⁄6.
Multiplying and Dividing Fractions Greater Than 1
Multiplying and dividing fractions greater than 1 is similar to multiplying and dividing proper fractions. However, you need to follow some rules:
Multiplying Fractions: To multiply fractions greater than 1, follow these steps:
- Multiply the numerators.
- Multiply the denominators.
- Simplify the result.
Dividing Fractions: To divide fractions greater than 1, follow these steps:
- Invert the second fraction (i.e., flip the numerator and denominator).
- Multiply the fractions.
- Simplify the result.
Example: Multiply 3⁄2 and 2⁄3.
Step 1: Multiply the numerators: 3 × 2 = 6.
Step 2: Multiply the denominators: 2 × 3 = 6.
Step 3: Simplify the result: 6⁄6 = 1.
Practice Exercises
Practice is key to mastering fractions greater than 1. Here are some exercises to help you get started:
- Convert the following improper fractions to mixed numbers:
- 7⁄4
- 9⁄5
- 11⁄6
- Add the following fractions:
- 2⁄3 + 3⁄4
- 5⁄6 + 1⁄2
- 7⁄8 + 3⁄4
- Subtract the following fractions:
- 3⁄2 - 2⁄3
- 5⁄4 - 1⁄2
- 7⁄6 - 3⁄4
- Multiply the following fractions:
- 2⁄3 × 3⁄4
- 5⁄6 × 2⁄3
- 7⁄8 × 3⁄4
- Divide the following fractions:
- 3⁄2 ÷ 2⁄3
- 5⁄4 ÷ 1⁄2
- 7⁄6 ÷ 3⁄4
As you practice, you’ll become more comfortable working with fractions greater than 1. Remember to take your time and follow the rules outlined in this article.
Solutions to Practice Exercises
Here are the solutions to the practice exercises:
- Convert the following improper fractions to mixed numbers:
- 7⁄4 = 1 3⁄4
- 9⁄5 = 1 4⁄5
- 11⁄6 = 1 5⁄6
- Add the following fractions:
- 2⁄3 + 3⁄4 = 11⁄12
- 5⁄6 + 1⁄2 = 4⁄3
- 7⁄8 + 3⁄4 = 13⁄8
- Subtract the following fractions:
- 3⁄2 - 2⁄3 = 5⁄6
- 5⁄4 - 1⁄2 = 3⁄4
- 7⁄6 - 3⁄4 = 1⁄12
- Multiply the following fractions:
- 2⁄3 × 3⁄4 = 1⁄2
- 5⁄6 × 2⁄3 = 5⁄9
- 7⁄8 × 3⁄4 = 21⁄32
- Divide the following fractions:
- 3⁄2 ÷ 2⁄3 = 9⁄4
- 5⁄4 ÷ 1⁄2 = 5⁄2
- 7⁄6 ÷ 3⁄4 = 14⁄9
We hope these solutions help you check your work and understand fractions greater than 1 better.
What is the difference between a proper fraction and an improper fraction?
+
A proper fraction is a fraction where the numerator is less than the denominator, whereas an improper fraction is a fraction where the numerator is greater than or equal to the denominator.
How do I convert an improper fraction to a mixed number?
+
To convert an improper fraction to a mixed number, divide the numerator by the denominator and write the remainder as a fraction.
What is the least common multiple (LCM) of two numbers?
+
The LCM of two numbers is the smallest number that is a multiple of both numbers.
Related Terms:
- Fractions worksheets PDF
- Fractions worksheets with answers PDF
- Free fraction worksheets with answers
- Fractions exercises with answers