5 Ways to Find Slope From a Table

Understanding Slope
Slope is a fundamental concept in mathematics, particularly in algebra and geometry. It represents the ratio of the vertical change (rise) to the horizontal change (run) between two points on a line. In other words, slope measures how steep a line is. There are several ways to find the slope of a line, and one of the most common methods is by using a table of values.
What is a Table of Values?
A table of values is a set of ordered pairs that represent points on a line. Each ordered pair consists of an input value (usually represented by x) and a corresponding output value (usually represented by y). The table of values can be used to visualize the relationship between the input and output values, making it easier to find the slope of the line.
Method 1: Finding Slope Using the Formula
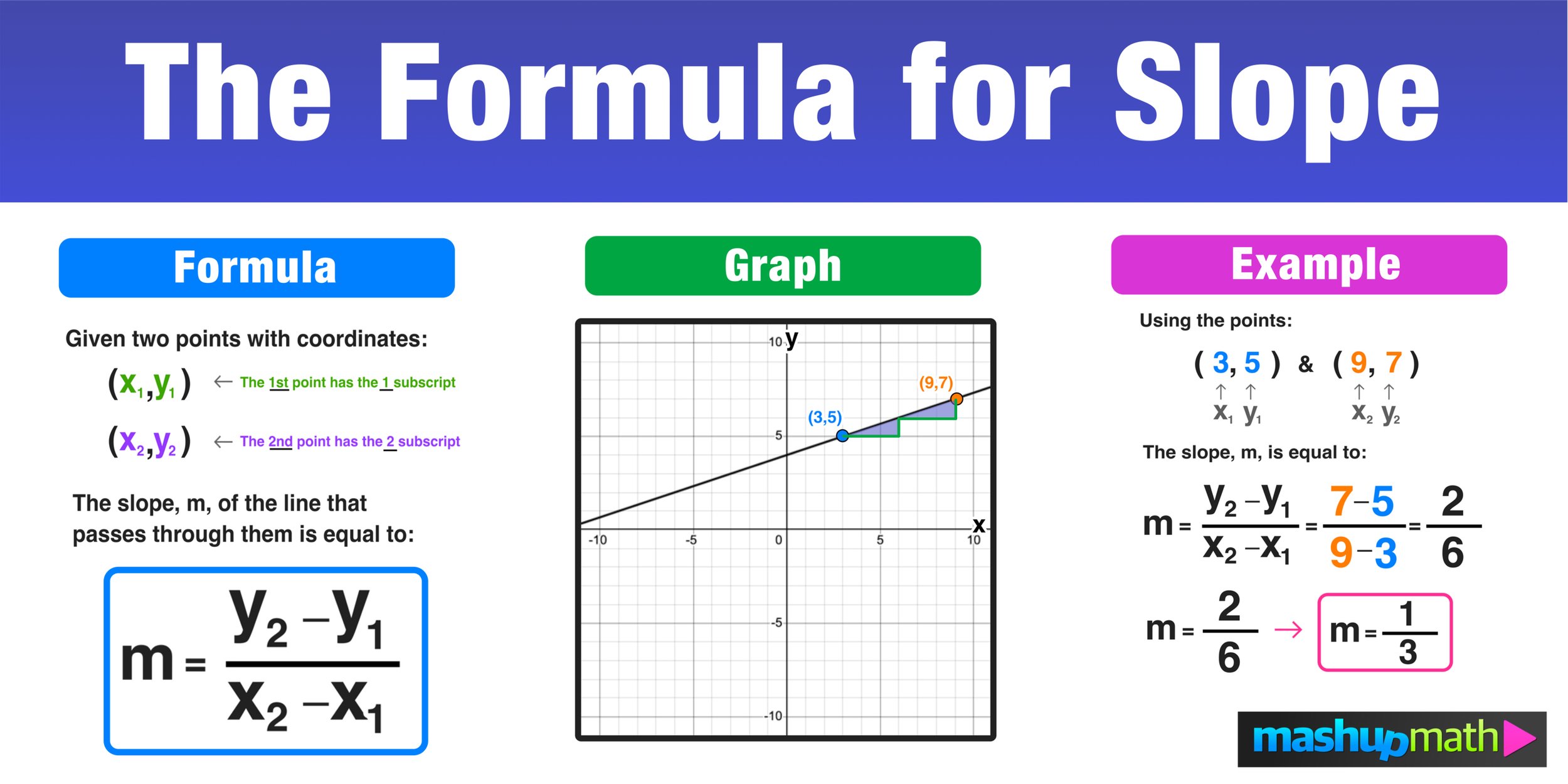
The formula for finding slope is:
Slope (m) = (y2 - y1) / (x2 - x1)
where (x1, y1) and (x2, y2) are two points on the line.
To find the slope using a table of values, simply choose two points from the table and plug them into the formula.
For example, let’s say we have the following table of values:
| x | y |
|---|---|
| 2 | 4 |
| 4 | 6 |
| 6 | 8 |
We can choose the points (2, 4) and (4, 6) to find the slope:
m = (6 - 4) / (4 - 2) m = 2 / 2 m = 1
Therefore, the slope of the line is 1.
📝 Note: Make sure to choose two points that are not identical, as this would result in a division by zero error.
Method 2: Finding Slope Using the Graph
Another way to find the slope of a line from a table of values is by graphing the points on a coordinate plane.
For example, let’s say we have the following table of values:
| x | y |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
We can plot the points on a coordinate plane:
By examining the graph, we can see that the line passes through the points (1, 2), (2, 4), and (3, 6). We can use the slope formula to find the slope:
m = (6 - 2) / (3 - 1) m = 4 / 2 m = 2
Therefore, the slope of the line is 2.
Method 3: Finding Slope Using the Rise Over Run Method
The rise over run method involves finding the vertical change (rise) and the horizontal change (run) between two points on the line.
For example, let’s say we have the following table of values:
| x | y |
|---|---|
| 2 | 4 |
| 4 | 6 |
| 6 | 8 |
We can choose the points (2, 4) and (4, 6) to find the slope:
- Rise: 6 - 4 = 2
- Run: 4 - 2 = 2
m = rise / run m = 2 / 2 m = 1
Therefore, the slope of the line is 1.
Method 4: Finding Slope Using the Table of Values with a Constant Rate of Change
If the table of values represents a line with a constant rate of change, we can find the slope by examining the pattern of the output values.
For example, let’s say we have the following table of values:
| x | y |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 8 |
We can see that for every increase in x by 1, the output value y increases by 2. This represents a constant rate of change, and we can find the slope:
m = 2 / 1 m = 2
Therefore, the slope of the line is 2.
Method 5: Finding Slope Using the Slope-Intercept Form
The slope-intercept form of a linear equation is y = mx + b, where m is the slope and b is the y-intercept.
If we have a table of values that represents a line in slope-intercept form, we can find the slope by examining the coefficient of x.
For example, let’s say we have the following table of values:
| x | y |
|---|---|
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
We can see that the output value y is equal to 2x + 1. Therefore, the slope is:
m = 2
Therefore, the slope of the line is 2.
In conclusion, there are several ways to find the slope of a line from a table of values, including using the formula, graphing the points, using the rise over run method, examining the pattern of the output values, and using the slope-intercept form.
What is the slope of a line?
+
The slope of a line is a measure of how steep it is. It is calculated as the ratio of the vertical change (rise) to the horizontal change (run) between two points on the line.
How do I find the slope of a line from a table of values?
+
There are several ways to find the slope of a line from a table of values, including using the formula, graphing the points, using the rise over run method, examining the pattern of the output values, and using the slope-intercept form.
What is the rise over run method?
+
The rise over run method involves finding the vertical change (rise) and the horizontal change (run) between two points on the line. The slope is then calculated as the rise divided by the run.