5 Ways to Find Missing Angles in Triangles
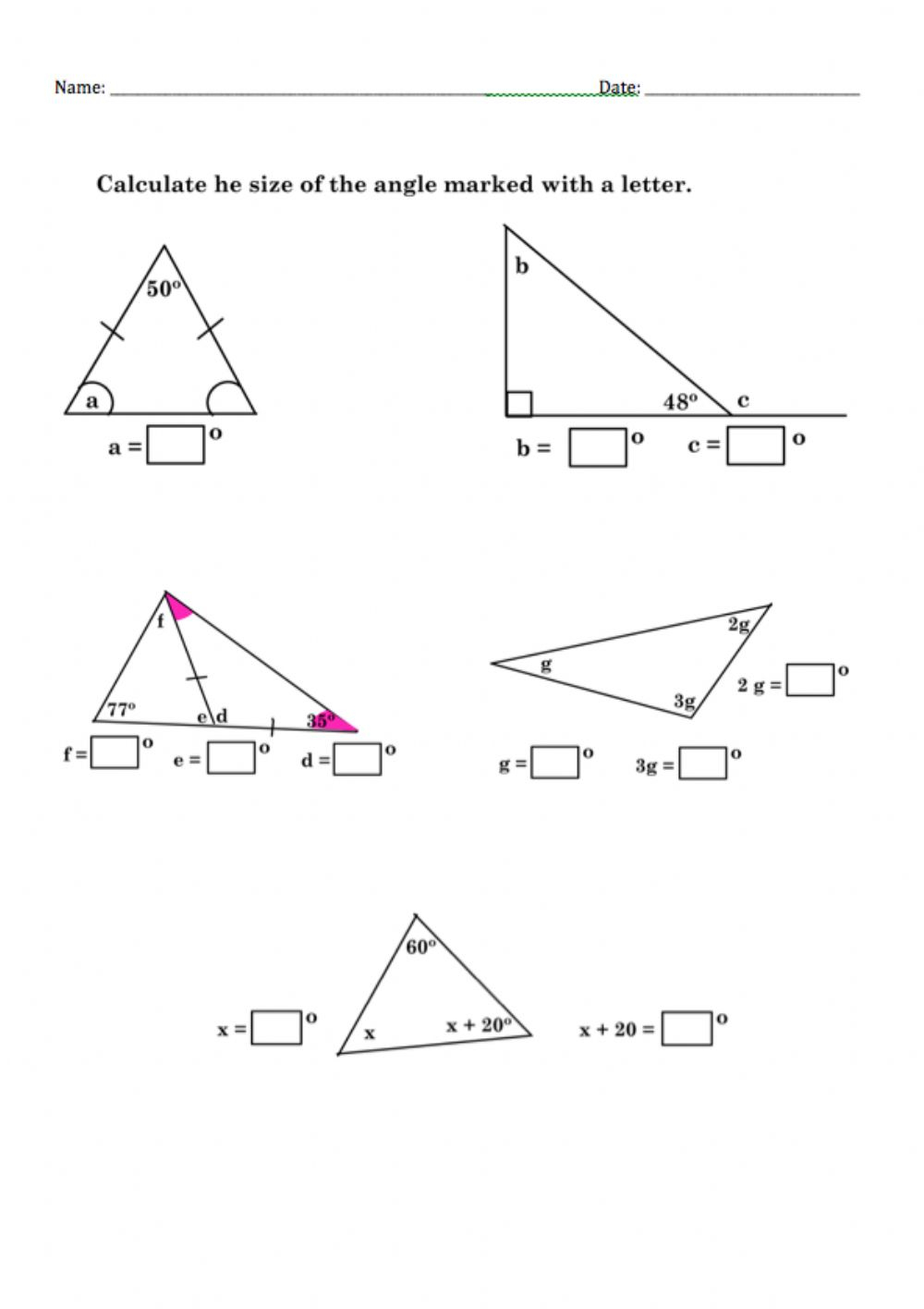
Understanding Angles in Triangles
Triangles are one of the most fundamental shapes in geometry, and understanding their properties is crucial for various mathematical and real-world applications. One of the key properties of triangles is the relationship between their angles. In this blog post, we will explore five ways to find missing angles in triangles.
The Basics of Triangle Angles
A triangle has three angles, and the sum of these angles is always 180 degrees. This property is known as the Angle Sum Property. To find a missing angle in a triangle, we need to know the measures of the other two angles.
Method 1: Using the Angle Sum Property
If we know the measures of two angles in a triangle, we can use the Angle Sum Property to find the third angle.
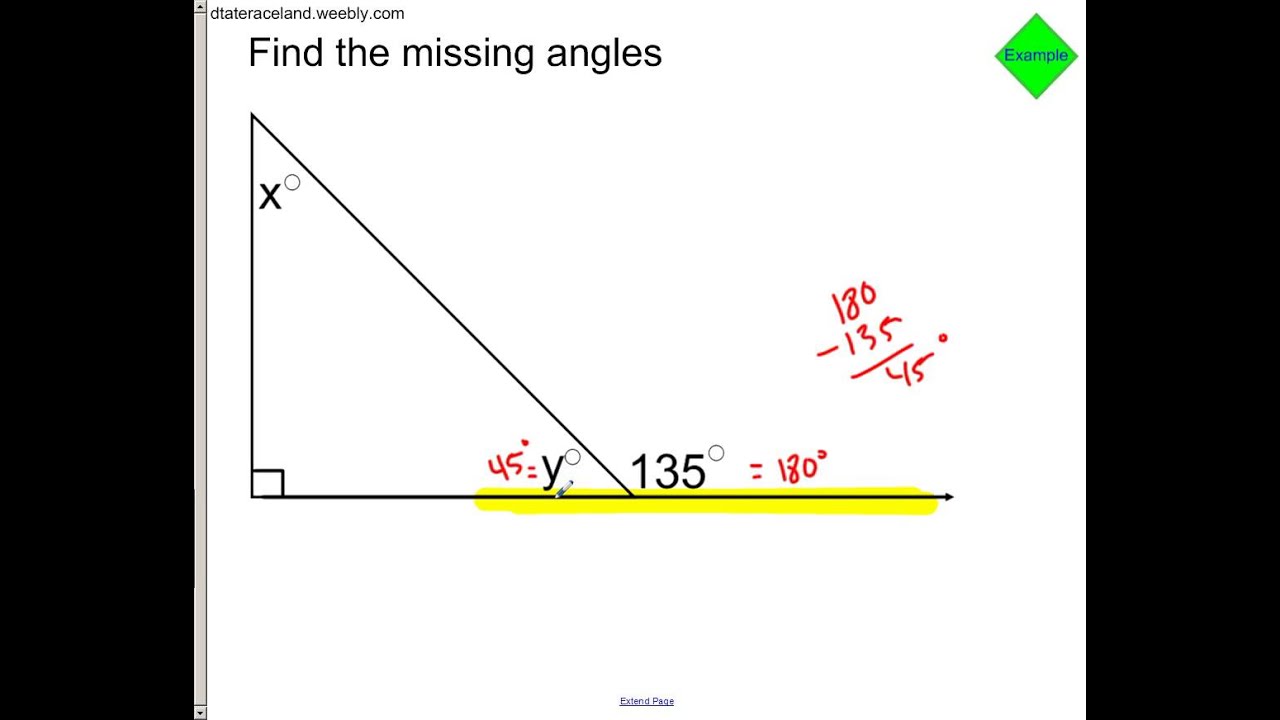
| Angle 1 | Angle 2 | Angle 3 (Missing) |
|---|---|---|
| 60° | 80° | x |
To find the missing angle, we add the measures of the two known angles and subtract the sum from 180°.
x = 180° - 60° - 80° x = 40°
Therefore, the missing angle measures 40°.
📝 Note: Make sure to check if the angles are in the correct units. In this case, we are working with degrees.
Method 2: Using Supplementary Angles
Supplementary angles are two angles whose measures add up to 180°. If we know one angle in a triangle and its supplementary angle, we can find the missing angle.
| Angle 1 | Angle 2 (Supplementary) | Angle 3 (Missing) |
|---|---|---|
| 60° | 120° | x |
Since the supplementary angle is 120°, we know that the missing angle is the complement of 120°.
x = 180° - 120° x = 60°
However, this is not the only possible solution. We need to consider the other angle in the triangle as well.
x = 180° - 60° - 120° x = 0°
This is not a valid solution, as the angle cannot be 0°. Therefore, the only possible solution is:
x = 60°
Method 3: Using Complementary Angles
Complementary angles are two angles whose measures add up to 90°. If we know one angle in a triangle and its complementary angle, we can find the missing angle.
| Angle 1 | Angle 2 (Complementary) | Angle 3 (Missing) |
|---|---|---|
| 30° | 60° | x |
Since the complementary angle is 60°, we know that the missing angle is the supplement of 60°.
x = 180° - 60° x = 120°
However, this is not the only possible solution. We need to consider the other angle in the triangle as well.
x = 180° - 30° - 60° x = 90°
Therefore, the missing angle measures 90°.
Method 4: Using Isosceles Triangles
An isosceles triangle has two equal sides, and the angles opposite these sides are also equal. If we know one angle in an isosceles triangle, we can find the missing angle.
| Angle 1 | Angle 2 (Equal) | Angle 3 (Missing) |
|---|---|---|
| 40° | 40° | x |
Since the two angles are equal, we know that the missing angle is the complement of 40°.
x = 180° - 40° - 40° x = 100°
Therefore, the missing angle measures 100°.
Method 5: Using Exterior Angles
An exterior angle of a triangle is an angle formed by one side of the triangle and the extension of an adjacent side. If we know one angle in a triangle and its exterior angle, we can find the missing angle.
| Angle 1 | Angle 2 (Exterior) | Angle 3 (Missing) |
|---|---|---|
| 50° | 130° | x |
Since the exterior angle is 130°, we know that the missing angle is the complement of 130°.
x = 180° - 130° x = 50°
However, this is not the only possible solution. We need to consider the other angle in the triangle as well.
x = 180° - 50° - 130° x = 0°
This is not a valid solution, as the angle cannot be 0°. Therefore, the only possible solution is:
x = 50°
And that’s it! We have explored five ways to find missing angles in triangles. Whether you’re using the Angle Sum Property, supplementary angles, complementary angles, isosceles triangles, or exterior angles, these methods will help you solve triangle problems with ease.
In conclusion, finding missing angles in triangles is a fundamental skill in geometry, and there are multiple methods to solve these problems. By applying the methods outlined in this blog post, you’ll be able to tackle triangle problems with confidence.
What is the Angle Sum Property?
+The Angle Sum Property states that the sum of the measures of the three angles in a triangle is always 180°.
What is a supplementary angle?
+A supplementary angle is an angle whose measure adds up to 180° when combined with another angle.
What is a complementary angle?
+A complementary angle is an angle whose measure adds up to 90° when combined with another angle.