6 Ways to Find Area of Irregular Shapes Easily

Introduction to Finding the Area of Irregular Shapes

Calculating the area of irregular shapes can be a daunting task, especially for those who are not familiar with the concept. Unlike regular shapes like squares, rectangles, and triangles, irregular shapes do not have standard formulas to calculate their areas. However, there are several methods and techniques that can help you find the area of irregular shapes easily. In this article, we will explore six ways to calculate the area of irregular shapes, making it easier for you to solve problems and complete projects.

Method 1: Divide the Shape into Smaller Regular Shapes

One of the simplest ways to find the area of an irregular shape is to divide it into smaller regular shapes. This method is useful when the irregular shape can be divided into recognizable shapes like triangles, rectangles, or squares. By calculating the area of each smaller shape and adding them up, you can find the total area of the irregular shape.

For example, let’s say you have an irregular shape that can be divided into two triangles and a rectangle. To find the area of the shape, you would calculate the area of each triangle and the rectangle separately and then add them up.

Area of Triangle 1: ½ × base × height = ½ × 5 × 6 = 15 square units Area of Triangle 2: ½ × base × height = ½ × 4 × 8 = 16 square units Area of Rectangle: length × width = 6 × 4 = 24 square units Total Area: 15 + 16 + 24 = 55 square units

Method 2: Use the Shoelace Formula

The shoelace formula is a mathematical formula used to calculate the area of a polygon when its vertices are given. The formula is useful for finding the area of irregular shapes with straight edges. To use the shoelace formula, you need to know the coordinates of the vertices of the shape.

The shoelace formula is:

Area = ½ |(x1y2 + x2y3 + … + xn-1yn + xn y1) - (y1x2 + y2x3 + … + yn-1xn + yn x1)|

where (x1, y1), (x2, y2), …, (xn, yn) are the coordinates of the vertices of the shape.

For example, let’s say you have a polygon with vertices (0, 0), (3, 4), (6, 2), and (2, 5). To find the area of the polygon, you would use the shoelace formula:

Area = ½ |(0 × 4 + 3 × 2 + 6 × 5 + 2 × 0) - (0 × 3 + 4 × 6 + 2 × 2 + 5 × 0)| Area = ½ |(0 + 6 + 30 + 0) - (0 + 24 + 4 + 0)| Area = ½ |36 - 28| Area = ½ |8| Area = 4 square units

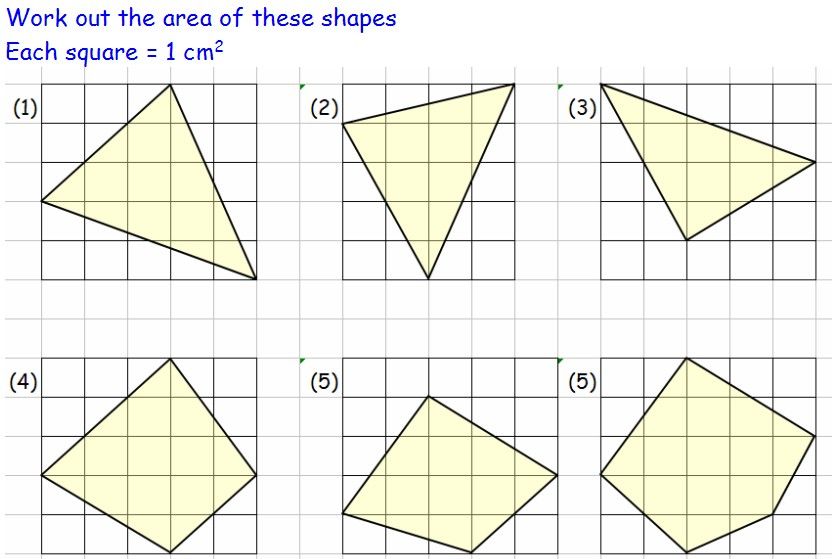
Method 3: Use the Grid Method

The grid method is a simple and visual way to estimate the area of an irregular shape. To use the grid method, you need to draw a grid over the shape and count the number of squares that cover the shape. Each square in the grid represents a unit area.

For example, let’s say you have an irregular shape that covers 12 squares in a grid. To find the area of the shape, you would multiply the number of squares by the area of each square.

Area = number of squares × area of each square Area = 12 × 1 square unit Area = 12 square units

Method 4: Use the Decomposition Method

The decomposition method involves breaking down an irregular shape into smaller, recognizable shapes that can be easily calculated. This method is useful when the irregular shape can be divided into recognizable shapes like triangles, rectangles, or squares.

For example, let’s say you have an irregular shape that can be divided into a triangle and a rectangle. To find the area of the shape, you would calculate the area of each smaller shape and add them up.

Area of Triangle: ½ × base × height = ½ × 5 × 6 = 15 square units Area of Rectangle: length × width = 6 × 4 = 24 square units Total Area: 15 + 24 = 39 square units

Method 5: Use the Approximation Method

The approximation method involves approximating the area of an irregular shape by using a known shape that closely resembles it. This method is useful when the irregular shape is close to a regular shape, such as a circle or an ellipse.

For example, let’s say you have an irregular shape that closely resembles a circle. To find the area of the shape, you would calculate the area of the circle and use it as an approximation.

Area of Circle: πr^2 = 3.14 × (4)^2 = 50.24 square units Approximate Area of Shape: 50.24 square units

Method 6: Use a Calculus Method

The calculus method involves using calculus to find the area of an irregular shape. This method is useful when the shape is defined by a mathematical function.

For example, let’s say you have a shape defined by the function y = x^2. To find the area of the shape, you would use the definite integral:

Area = ∫[0, 4] x^2 dx Area = (¹⁄₃)x^3 | [0, 4] Area = (¹⁄₃)(4)^3 - (¹⁄₃)(0)^3 Area = ⁶⁴⁄₃ square units

📝 Note: The calculus method is a more advanced method that requires knowledge of calculus. It is not recommended for beginners.

Conclusion

Calculating the area of irregular shapes can be challenging, but there are several methods and techniques that can help. By using one or a combination of the methods described in this article, you can easily find the area of irregular shapes. Remember to choose the method that best suits the shape you are working with, and don’t be afraid to use approximation methods when necessary.