Find the Slope of Each Line Made Easy

Understanding the Concept of Slope

The slope of a line is a measure of how steep it is. It is defined as the ratio of the vertical change (rise) to the horizontal change (run) between two points on the line. In simpler terms, it tells you how much the line rises (or falls) for every unit you move to the right.

Why is Slope Important?

Slope is a crucial concept in mathematics, particularly in algebra and geometry. It is used to describe the steepness of a line, which is essential in various real-world applications, such as:

• Physics and Engineering: Slope is used to calculate the velocity and acceleration of objects.
• Economics: Slope is used to analyze the relationship between variables, such as supply and demand.
• Computer Science: Slope is used in machine learning algorithms to analyze data.

How to Find the Slope of a Line

There are several ways to find the slope of a line, depending on the information you have. Here are some common methods:

Method 1: Using Two Points

If you have two points on the line, you can use the slope formula:

Slope (m) = (y2 - y1) / (x2 - x1)

Where (x1, y1) and (x2, y2) are the coordinates of the two points.

Example:

Find the slope of the line passing through points (2, 3) and (4, 5).

m = (5 - 3) / (4 - 2) = 2 / 2 = 1

Method 2: Using the Slope-Intercept Form

If the equation of the line is in slope-intercept form (y = mx + b), you can easily find the slope by identifying the coefficient of x.

Example:

Find the slope of the line with equation y = 2x + 3.

The slope is the coefficient of x, which is 2.

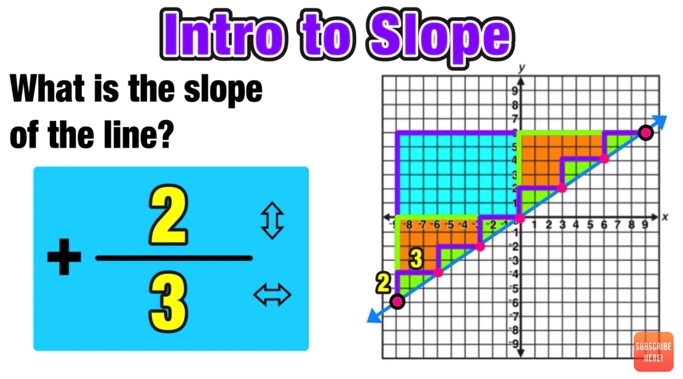
Method 3: Using the Graph

If you have a graph of the line, you can find the slope by counting the rise and run between two points on the line.

Example:

Find the slope of the line graphed below.

The rise is 3 units, and the run is 2 units. Therefore, the slope is:

m = 3 / 2 = 1.5

Notes

• 📝 Note: When finding the slope using two points, it doesn’t matter which point you call (x1, y1) and which point you call (x2, y2). The slope will be the same either way.

• 📝 Note: If the line is horizontal (i.e., it doesn’t rise or fall), the slope is 0. If the line is vertical (i.e., it rises or falls infinitely), the slope is undefined.

Finding the slope of a line is a fundamental concept in mathematics. By mastering the different methods, you’ll be able to analyze and work with linear relationships with confidence.

Summing Up

In this article, we’ve covered the concept of slope and its importance in various fields. We’ve also discussed three methods for finding the slope of a line: using two points, using the slope-intercept form, and using the graph. With practice and patience, you’ll become proficient in finding the slope of any line.