Master Law of Cosines and Sines in 5 Easy Steps
Understanding the Law of Cosines and Sines
The Law of Cosines and Sines are two fundamental concepts in trigonometry that help us solve triangles. While they may seem intimidating at first, mastering these laws can be a game-changer for anyone who wants to become proficient in trigonometry. In this article, we’ll break down the Law of Cosines and Sines into 5 easy steps, making it easy for you to understand and apply them.
Step 1: Understanding the Law of Cosines
The Law of Cosines is a formula that relates the lengths of the sides of a triangle to the cosine of one of its angles. The formula is:
c² = a² + b² - 2ab * cos©
where:
- c is the length of the side opposite angle C
- a and b are the lengths of the other two sides
- C is the angle opposite side c
This formula is useful when we know the lengths of two sides and the included angle, and we want to find the length of the third side.
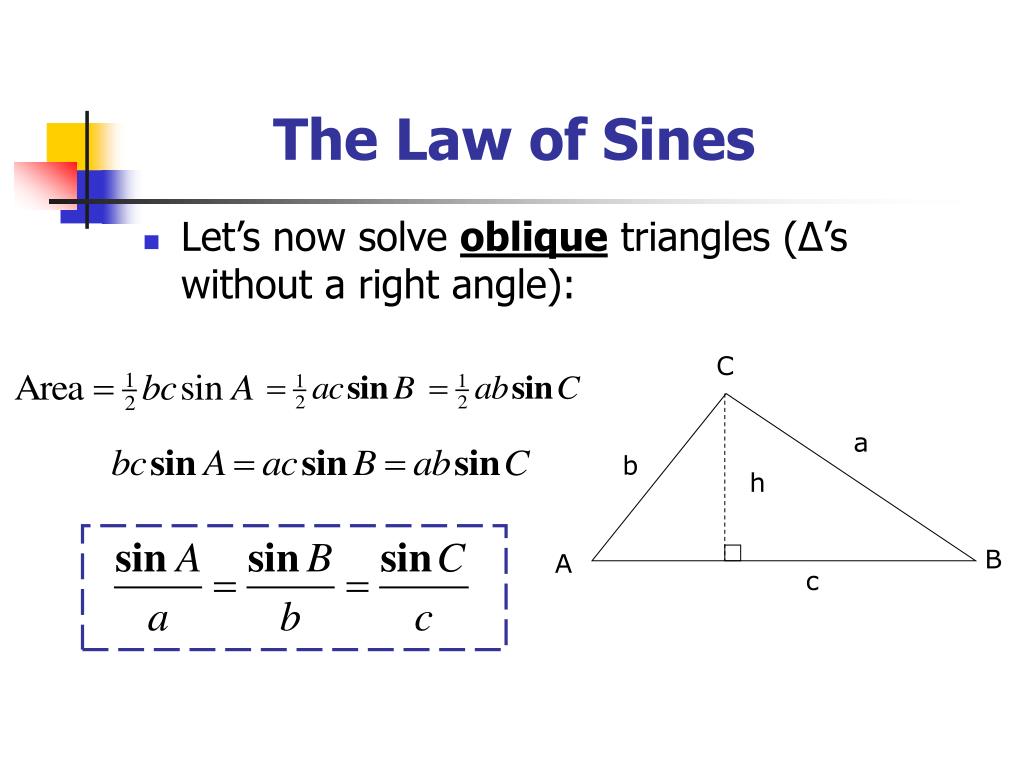
Step 2: Understanding the Law of Sines
The Law of Sines is a formula that relates the lengths of the sides of a triangle to the sines of its angles. The formula is:
a / sin(A) = b / sin(B) = c / sin©
where:
- a, b, and c are the lengths of the sides
- A, B, and C are the angles opposite sides a, b, and c
This formula is useful when we know the length of one side and the angle opposite it, and we want to find the lengths of the other sides.
Step 3: Applying the Law of Cosines
Now that we’ve covered the formulas, let’s see how to apply them. Suppose we have a triangle with sides a, b, and c, and angle C opposite side c. We can use the Law of Cosines to find the length of side c.
For example, if we know that a = 3, b = 4, and angle C = 60°, we can plug these values into the formula:
c² = 3² + 4² - 2(3)(4) * cos(60°) c² = 9 + 16 - 24 * 0.5 c² = 25 - 12 c² = 13 c = √13
Therefore, the length of side c is √13.
📝 Note: Make sure to check the units of the sides and angles when applying the formulas.
Step 4: Applying the Law of Sines
Now let’s see how to apply the Law of Sines. Suppose we have a triangle with sides a, b, and c, and angle A opposite side a. We can use the Law of Sines to find the length of side b.
For example, if we know that a = 2, angle A = 30°, and angle B = 60°, we can plug these values into the formula:
2 / sin(30°) = b / sin(60°) 2 / 0.5 = b / 0.866 b = 2 * 0.866 / 0.5 b = 3.46
Therefore, the length of side b is approximately 3.46.
Step 5: Practice, Practice, Practice!
The key to mastering the Law of Cosines and Sines is to practice, practice, practice! Try solving different types of triangles using these formulas. Start with simple problems and gradually move on to more complex ones.

| Problem Type | Example |
|---|---|
| SAS (Side-Angle-Side) | Find the length of side c in a triangle with sides a = 3, b = 4, and angle C = 60°. |
| SSS (Side-Side-Side) | Find the angles of a triangle with sides a = 2, b = 3, and c = 4. |
| ASA (Angle-Side-Angle) | Find the length of side b in a triangle with angle A = 30°, angle B = 60°, and side a = 2. |
By following these 5 easy steps, you’ll become proficient in using the Law of Cosines and Sines to solve triangles. Remember to practice regularly and apply these formulas to different types of problems.
In conclusion, the Law of Cosines and Sines are powerful tools for solving triangles. By understanding these formulas and practicing their application, you’ll become a master of trigonometry in no time.
What is the difference between the Law of Cosines and the Law of Sines?
+The Law of Cosines is used to find the length of the third side of a triangle when we know the lengths of two sides and the included angle. The Law of Sines is used to find the lengths of the sides of a triangle when we know the length of one side and the angle opposite it.
How do I know which formula to use?
+Use the Law of Cosines when you know the lengths of two sides and the included angle. Use the Law of Sines when you know the length of one side and the angle opposite it.
Can I use these formulas to solve all types of triangles?
+Yes, these formulas can be used to solve all types of triangles, including right triangles, oblique triangles, and obtuse triangles.



