7 Ways to Master Factoring by Grouping

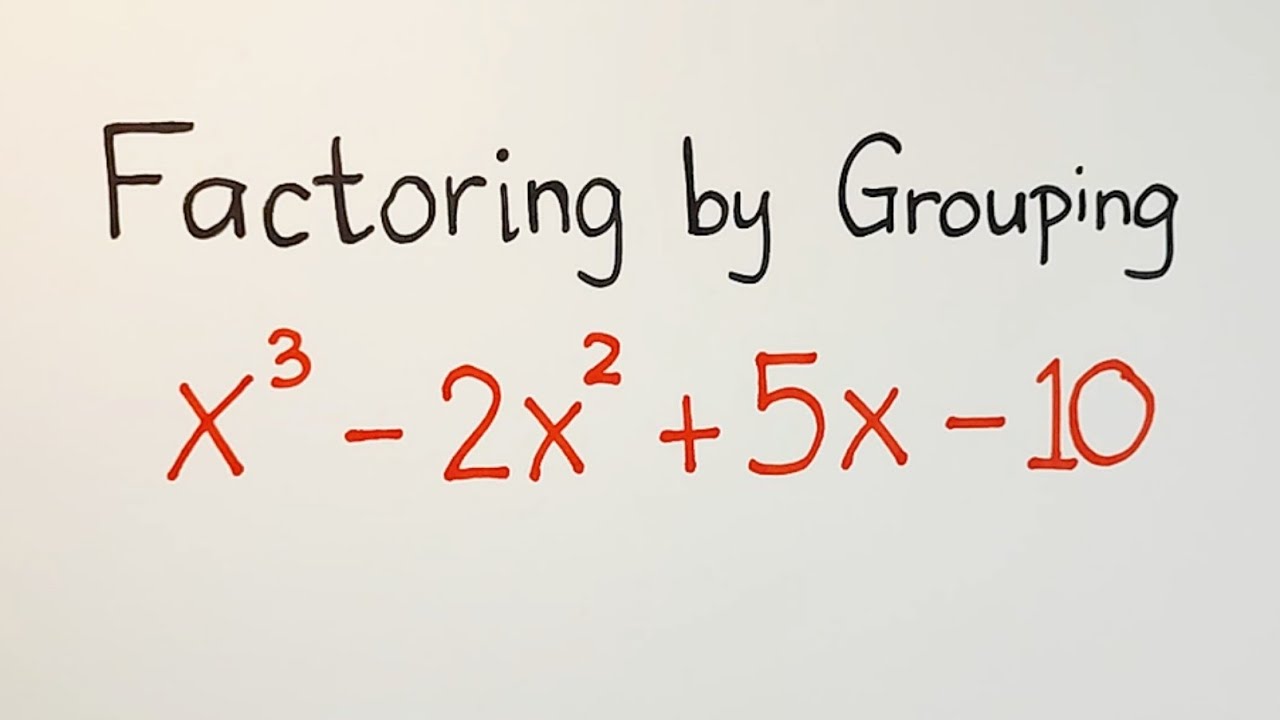
Unlocking the Power of Factoring by Grouping

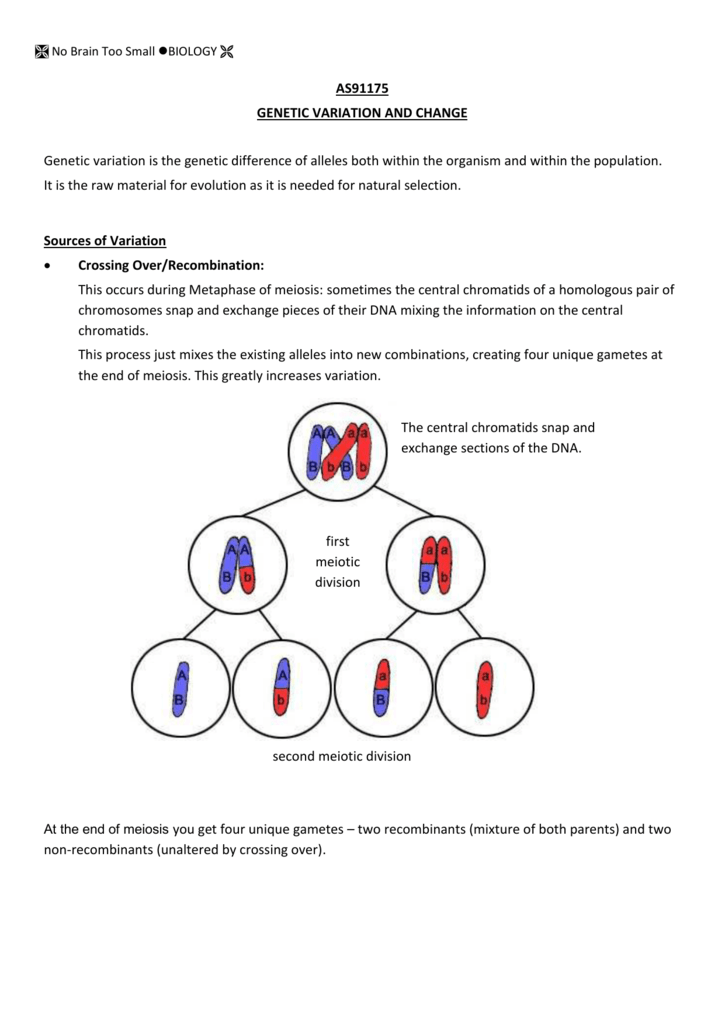
Factoring by grouping is a powerful technique used in algebra to factorize quadratic expressions. It involves grouping terms in a way that allows us to factor out common factors, making it easier to solve equations and simplify expressions. In this article, we will explore 7 ways to master factoring by grouping, along with examples, notes, and FAQs to help you become a pro in no time.

Understanding the Basics of Factoring by Grouping

Before we dive into the 7 ways to master factoring by grouping, let’s first understand the basics of this technique. Factoring by grouping involves grouping terms in a quadratic expression into pairs, such that each pair has a common factor. We then factor out this common factor, leaving us with a simpler expression.

Example:

Factor the following quadratic expression using factoring by grouping:

x^2 + 5x + 6

We can group the terms as follows:

(x^2 + 5x) + 6

Now, we can factor out the common factor of x from the first pair:

x(x + 5) + 6

Next, we can factor out the common factor of 1 from the second pair:

x(x + 5) + 1(6)

Finally, we can combine the two pairs:

x(x + 5) + 1(6) = x(x + 5) + 6

And that’s it! We have factored the quadratic expression using factoring by grouping.

7 Ways to Master Factoring by Grouping

Now that we understand the basics of factoring by grouping, let’s explore 7 ways to master this technique.

1. Identify the Common Factor

The first step in factoring by grouping is to identify the common factor among the terms. Look for the greatest common factor (GCF) of the coefficients of the terms.

Example:

Factor the following quadratic expression using factoring by grouping:

2x^2 + 6x + 4

The GCF of the coefficients is 2, so we can factor out 2 from each term:

2(x^2 + 3x + 2)

2. Group Terms into Pairs

Once we have identified the common factor, we can group the terms into pairs. Look for pairs of terms that have a common factor.

Example:

Factor the following quadratic expression using factoring by grouping:

x^2 + 4x + 3x + 12

We can group the terms as follows:

(x^2 + 4x) + (3x + 12)

Now, we can factor out the common factor of x from the first pair:

x(x + 4) + (3x + 12)

3. Factor Out the Common Factor

Now that we have grouped the terms into pairs, we can factor out the common factor from each pair.

Example:

Factor the following quadratic expression using factoring by grouping:

x^2 + 5x + 6

We can group the terms as follows:

(x^2 + 5x) + 6

Now, we can factor out the common factor of x from the first pair:

x(x + 5) + 6

4. Use the FOIL Method

The FOIL method is a technique used to multiply two binomials. We can use this method to factor quadratic expressions using factoring by grouping.

Example:

Factor the following quadratic expression using factoring by grouping:

x^2 + 6x + 8

We can group the terms as follows:

(x^2 + 6x) + 8

Now, we can use the FOIL method to factor the first pair:

x(x + 6) + 8

5. Look for Patterns

When factoring by grouping, look for patterns in the coefficients of the terms. If we can identify a pattern, we can use it to factor the expression.

Example:

Factor the following quadratic expression using factoring by grouping:

x^2 + 2x + x + 2

We can group the terms as follows:

(x^2 + 2x) + (x + 2)

Now, we can factor out the common factor of x from the first pair:

x(x + 2) + (x + 2)

6. Use the AC Method

The AC method is a technique used to factor quadratic expressions. We can use this method to factor expressions using factoring by grouping.

Example:

Factor the following quadratic expression using factoring by grouping:

x^2 + 5x + 6

We can group the terms as follows:

(x^2 + 5x) + 6

Now, we can use the AC method to factor the first pair:

x(x + 5) + 6

7. Practice, Practice, Practice

Finally, the key to mastering factoring by grouping is to practice, practice, practice. The more you practice, the more comfortable you will become with this technique.

👍 Note: Factoring by grouping can be a challenging technique to master, but with practice and patience, you can become a pro in no time.

Notes:

• When factoring by grouping, make sure to identify the common factor among the terms.
• Group terms into pairs, and factor out the common factor from each pair.
• Use the FOIL method, look for patterns, and use the AC method to help you factor expressions.
• Practice, practice, practice to become more comfortable with this technique.

Conclusion

Factoring by grouping is a powerful technique used in algebra to factorize quadratic expressions. By following the 7 ways to master factoring by grouping, you can become a pro in no time. Remember to identify the common factor, group terms into pairs, factor out the common factor, use the FOIL method, look for patterns, use the AC method, and practice, practice, practice.