Equivalent Fractions Using Multiplication Worksheet

Understanding Equivalent Fractions Using Multiplication
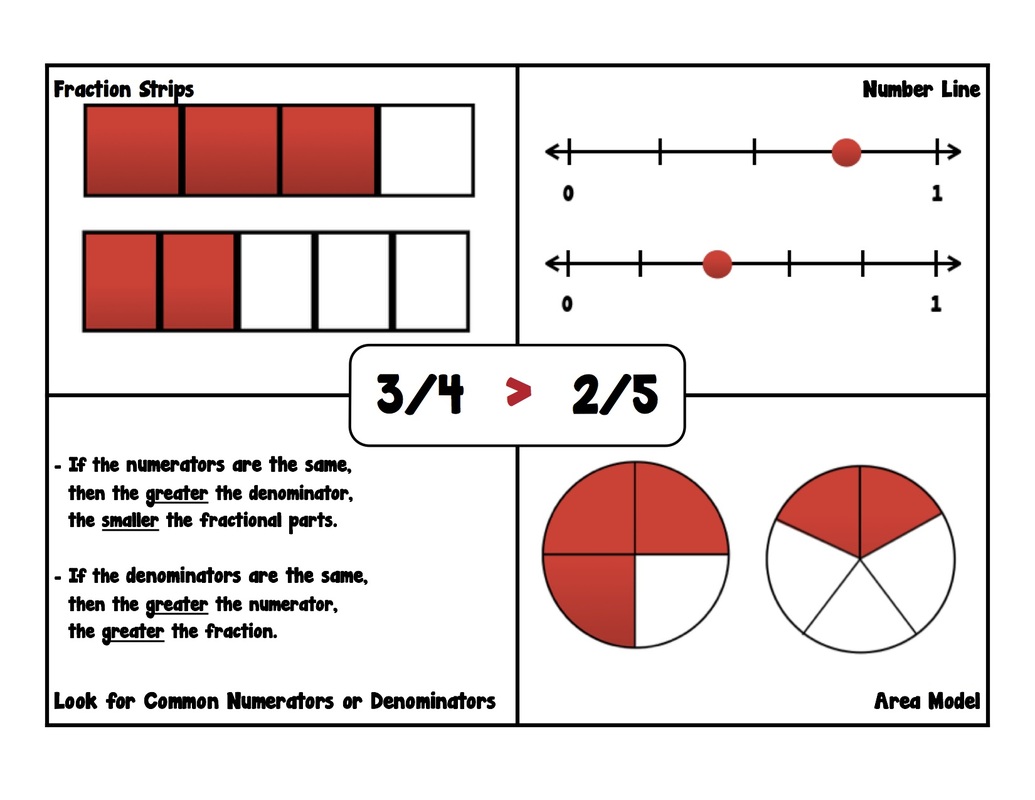
Equivalent fractions are fractions that represent the same value, even if their numerators and denominators differ. One way to find equivalent fractions is by multiplying the numerator and denominator by the same number. In this article, we will explore how to use multiplication to find equivalent fractions and provide a worksheet to practice this concept.
Why Multiply to Find Equivalent Fractions?
Multiplying the numerator and denominator of a fraction by the same number does not change the value of the fraction. This is because multiplying by a number is equivalent to adding a number of copies of itself together. For example, 2 × 3 is the same as 2 + 2 + 2. Therefore, if you multiply the numerator and denominator by the same number, you are essentially adding the same number of copies of itself together, which does not change the value of the fraction.
How to Multiply to Find Equivalent Fractions
To find equivalent fractions using multiplication, follow these steps:
- Choose a number to multiply the numerator and denominator by.
- Multiply the numerator by the chosen number.
- Multiply the denominator by the chosen number.
- Write the new numerator and denominator as an equivalent fraction.
For example, let’s find an equivalent fraction for 1⁄2 by multiplying the numerator and denominator by 3:
- Choose a number to multiply: 3
- Multiply the numerator: 1 × 3 = 3
- Multiply the denominator: 2 × 3 = 6
- Write the new fraction: 3⁄6
The fraction 3⁄6 is equivalent to 1⁄2 because they represent the same value.
Equivalent Fractions Using Multiplication Worksheet
Here is a worksheet to practice finding equivalent fractions using multiplication:
Part 1: Find Equivalent Fractions
Find an equivalent fraction for each of the following fractions by multiplying the numerator and denominator by the number in parentheses.
| Fraction | Multiply by |
|---|---|
| 1⁄2 | 2 |
| 2⁄3 | 4 |
| 3⁄4 | 5 |
| 1⁄3 | 6 |
| 2⁄5 | 3 |
Part 2: Create Your Own Equivalent Fractions
Create three equivalent fractions for each of the following fractions by multiplying the numerator and denominator by different numbers.
| Fraction | Equivalent Fractions |
|---|---|
| 1⁄2 | |
| 2⁄3 | |
| 3⁄4 |
Answer Key
Part 1: Find Equivalent Fractions
| Fraction | Equivalent Fraction |
|---|---|
| 1⁄2 | 2⁄4 |
| 2⁄3 | 8⁄12 |
| 3⁄4 | 15⁄20 |
| 1⁄3 | 6⁄18 |
| 2⁄5 | 6⁄15 |
📝 Note: Remember to multiply the numerator and denominator by the same number to find equivalent fractions.
Common Multiples and Equivalent Fractions
When finding equivalent fractions, it’s essential to consider the least common multiple (LCM) of the denominators. The LCM is the smallest number that both denominators can divide into evenly. For example, the LCM of 2 and 4 is 4. By finding the LCM, you can determine the simplest equivalent fraction.
Real-World Applications of Equivalent Fractions
Equivalent fractions have many real-world applications, such as:
- Cooking: Recipes often require equivalent fractions of ingredients.
- Building: Architects use equivalent fractions to scale blueprints.
- Finance: Equivalent fractions are used to calculate interest rates and investment returns.
In conclusion, equivalent fractions are a fundamental concept in mathematics, and using multiplication is a straightforward method to find them. By practicing with the worksheet provided, you will become more comfortable with finding equivalent fractions and applying them to real-world problems.
What is an equivalent fraction?
+An equivalent fraction is a fraction that represents the same value as another fraction, even if the numerator and denominator differ.
Why is multiplying the numerator and denominator by the same number important?
+Multiplying the numerator and denominator by the same number does not change the value of the fraction, making it possible to find equivalent fractions.
What is the least common multiple (LCM), and why is it important in finding equivalent fractions?
+The LCM is the smallest number that both denominators can divide into evenly. Finding the LCM helps determine the simplest equivalent fraction.
Related Terms:
- Comparing fractions Worksheet
- Equivalent fractions worksheet Year 4
- Equivalent fraction chains worksheets
- Equivalent fraction Worksheet grade 3