Equivalent Fractions Super Teacher Worksheets Simplified

Understanding Equivalent Fractions
Equivalent fractions are fractions that represent the same value, even though they may look different. These fractions have the same numerator and denominator ratio. In other words, they are equal in value, but their numerators and denominators may be different.
What are Equivalent Fractions?
Equivalent fractions are created by multiplying or dividing both the numerator and denominator of a fraction by the same number. For example, let’s consider the fraction 1⁄2. We can create an equivalent fraction by multiplying both the numerator and denominator by 2, resulting in 2⁄4. We can also create another equivalent fraction by multiplying both the numerator and denominator by 3, resulting in 3⁄6.
📝 Note: When multiplying or dividing both the numerator and denominator by the same number, the value of the fraction remains the same.
How to Find Equivalent Fractions
To find equivalent fractions, follow these steps:
- Start with a fraction.
- Multiply or divide both the numerator and denominator by the same number.
- The resulting fraction is equivalent to the original fraction.
For example, let’s find equivalent fractions for 1⁄2:
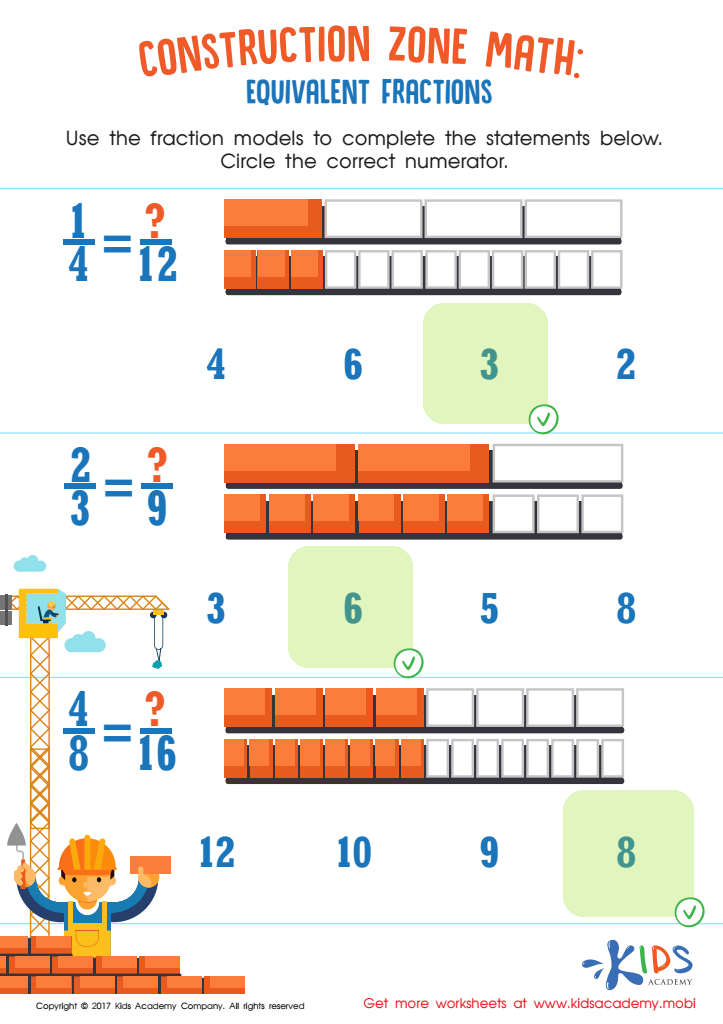
| Original Fraction | Multiplier | Equivalent Fraction |
|---|---|---|
| 1⁄2 | 2 | 2⁄4 |
| 1⁄2 | 3 | 3⁄6 |
| 1⁄2 | 4 | 4⁄8 |
| Original Fraction | Multiplier | Equivalent Fraction |
|---|---|---|
| 1/2 | 2 | 2/4 |
| 1/2 | 3 | 3/6 |
| 1/2 | 4 | 4/8 |
Why are Equivalent Fractions Important?
Equivalent fractions are important because they help us to:
- Simplify fractions: Equivalent fractions can be used to simplify complex fractions.
- Compare fractions: Equivalent fractions make it easier to compare fractions with different denominators.
- Add and subtract fractions: Equivalent fractions are necessary for adding and subtracting fractions with different denominators.
Real-World Applications of Equivalent Fractions
Equivalent fractions have many real-world applications, such as:
- Cooking: When a recipe calls for 1⁄4 cup of sugar, but you only have a 1⁄8 cup measuring cup, you can use equivalent fractions to determine how much sugar to use.
- Building design: Architects use equivalent fractions to ensure that buildings are constructed with proportional dimensions.
- Science: Equivalent fractions are used in scientific calculations, such as converting between units of measurement.
Common Mistakes to Avoid
When working with equivalent fractions, avoid the following common mistakes:
- Changing the numerator or denominator separately: This can change the value of the fraction.
- Forgetting to multiply or divide both the numerator and denominator: This can result in an incorrect equivalent fraction.
Conclusion
In conclusion, equivalent fractions are a fundamental concept in mathematics that can help us simplify, compare, and add and subtract fractions. By understanding how to find equivalent fractions, we can apply this knowledge to real-world situations and avoid common mistakes.
What are equivalent fractions?
+Equivalent fractions are fractions that represent the same value, even though they may look different.
How do I find equivalent fractions?
+To find equivalent fractions, multiply or divide both the numerator and denominator of a fraction by the same number.
Why are equivalent fractions important?
+Equivalent fractions are important because they help us simplify, compare, and add and subtract fractions.
Related Terms:
- Equivalent fractions Worksheet with answers
- Equivalent fractions game PDF
- Equivalent fractions PDF
- Worksheet fraction
- Fractions fun worksheets