Circle Equations Worksheet with Answers and Solutions
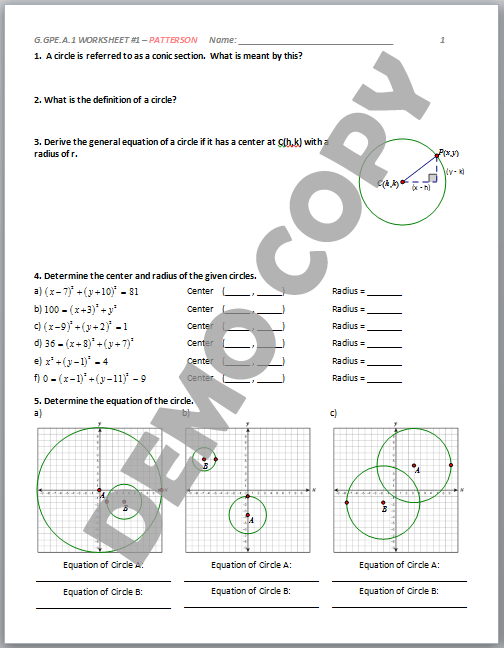
Understanding Circle Equations: A Comprehensive Guide
Circle equations are a fundamental concept in mathematics, particularly in geometry and trigonometry. They describe the relationship between the coordinates of a point on a circle and the circle’s center and radius. In this article, we will delve into the world of circle equations, exploring their forms, applications, and providing a worksheet with answers and solutions to help solidify your understanding.
The General Form of a Circle Equation
The general form of a circle equation is given by:
(x - h)^2 + (y - k)^2 = r^2
where:
- (x, y) represents the coordinates of a point on the circle
- (h, k) represents the coordinates of the circle’s center
- r represents the radius of the circle
Understanding the Components of the Circle Equation
To grasp the concept of circle equations, it’s essential to understand the role of each component:
- Center (h, k): The center of the circle is the point from which the radius is measured. It’s the point that is equidistant from all points on the circle.
- Radius ®: The radius is the distance from the center to any point on the circle. It’s a measure of the circle’s size.
Types of Circle Equations
There are two primary types of circle equations:
- Standard Form: This is the general form of the circle equation, which we discussed earlier.
- Graphing Form: This form is used to graph circles on a coordinate plane. It’s given by:
(x - h)^2 + (y - k)^2 = r^2
where the center (h, k) and radius ® are given.
Converting Between Standard and Graphing Forms
To convert a circle equation from standard form to graphing form, follow these steps:
- Expand the equation by multiplying out the squared terms.
- Rearrange the terms to isolate the x and y variables.
- Factor out the constants to obtain the graphing form.
Conversely, to convert a circle equation from graphing form to standard form, follow these steps:
- Multiply out the squared terms to expand the equation.
- Combine like terms.
- Write the equation in the standard form.
Circle Equations Worksheet with Answers and Solutions
Here’s a worksheet to help you practice working with circle equations:
Part 1: Multiple Choice Questions
- What is the center of the circle with equation (x - 2)^2 + (y + 3)^2 = 16? a) (2, -3) b) (-2, 3) c) (2, 3) d) (-2, -3)
Answer: a) (2, -3)
- What is the radius of the circle with equation (x + 1)^2 + (y - 2)^2 = 25? a) 3 b) 4 c) 5 d) 6
Answer: c) 5
Part 2: Short Answer Questions
- Write the equation of a circle with center (4, -2) and radius 3.
Answer: (x - 4)^2 + (y + 2)^2 = 9
- Convert the equation (x + 2)^2 + (y - 3)^2 = 16 to standard form.
Answer: (x + 2)^2 + (y - 3)^2 = 16 → x^2 + 4x + 4 + y^2 - 6y + 9 = 16 → x^2 + y^2 + 4x - 6y - 3 = 0
Part 3: Graphing Questions
- Graph the circle with equation (x - 1)^2 + (y + 2)^2 = 4.
Answer: (graph the circle with center (1, -2) and radius 2)
- Find the equation of the circle that passes through points (3, 4), (5, 6), and (7, 8).
Answer: (find the equation of the circle using the three points)
📝 Note: For graphing questions, use graph paper and plot the points accordingly.
Practice Tips and Tricks
- Always identify the center and radius of the circle when working with circle equations.
- Use the standard form to convert between standard and graphing forms.
- Practice graphing circles on a coordinate plane to visualize the equation.
Circle equations are a fundamental concept in mathematics, and with practice, you’ll become proficient in working with them. Remember to always identify the center and radius, and use the standard form to convert between forms. Happy practicing!
What is the difference between the standard form and graphing form of a circle equation?
+
The standard form of a circle equation is (x - h)^2 + (y - k)^2 = r^2, while the graphing form is used to graph circles on a coordinate plane. The graphing form is given by (x - h)^2 + (y - k)^2 = r^2, where the center (h, k) and radius ® are given.
How do I convert a circle equation from standard form to graphing form?
+
To convert a circle equation from standard form to graphing form, expand the equation by multiplying out the squared terms, rearrange the terms to isolate the x and y variables, and factor out the constants to obtain the graphing form.
What is the center of a circle with equation (x - 2)^2 + (y + 3)^2 = 16?
+
The center of the circle is (2, -3).
Related Terms:
- Circles Review Worksheet pdf
- Equations of Circles practice
- Tangent circle worksheet pdf
- Circle theorem worksheet