Domain and Range Worksheet 2 Answer Key
Understanding Domain and Range
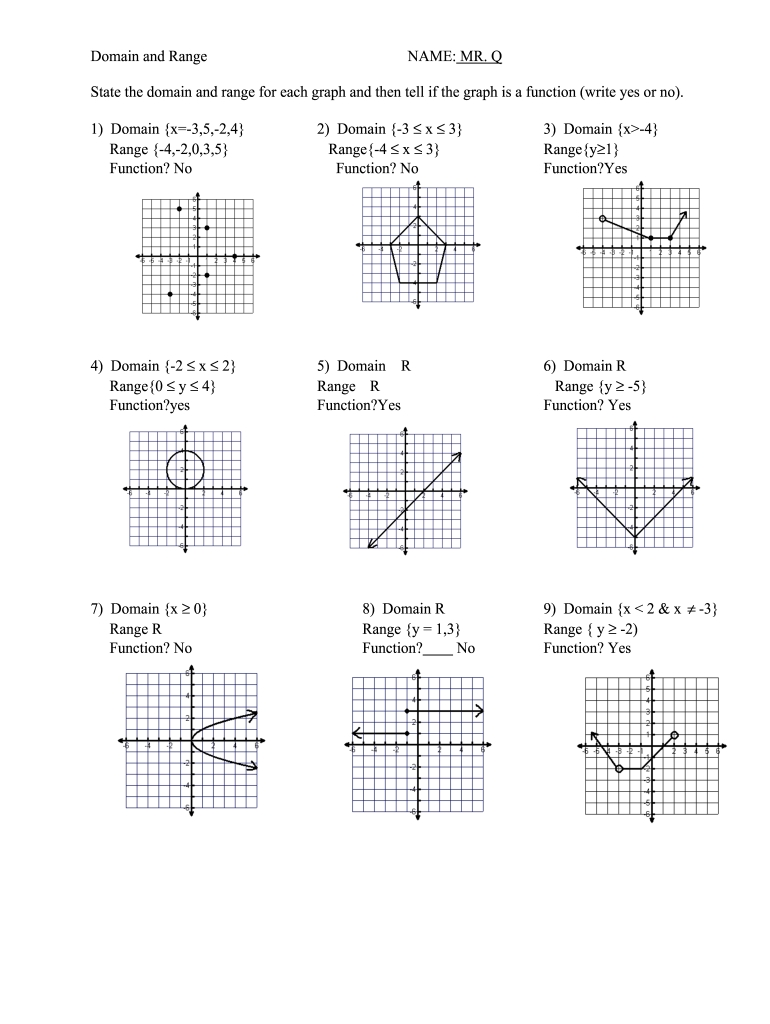
When working with functions, two important concepts to grasp are the domain and range. The domain of a function is the set of all possible input values for which the function is defined, while the range is the set of all possible output values. In this worksheet, we’ll explore how to determine the domain and range of various functions.
Functions and Their Domains
The domain of a function is the set of all input values for which the function produces a real number as output. There are several types of functions, and each has its own rules for determining the domain.
- Linear Functions: The domain of a linear function is all real numbers unless there is a restriction.
- Quadratic Functions: The domain of a quadratic function is all real numbers unless there is a restriction.
- Rational Functions: The domain of a rational function is all real numbers except where the denominator equals zero.
- Absolute Value Functions: The domain of an absolute value function is all real numbers unless there is a restriction.
Functions and Their Ranges
The range of a function is the set of all possible output values. The range depends on the type of function and its restrictions.
- Linear Functions: The range of a linear function is all real numbers unless there is a restriction.
- Quadratic Functions: The range of a quadratic function is all real numbers greater than or equal to the minimum value or less than or equal to the maximum value.
- Rational Functions: The range of a rational function is all real numbers except where the numerator equals zero.
- Absolute Value Functions: The range of an absolute value function is all real numbers greater than or equal to zero.
Domain and Range Worksheet 2 Answer Key
Section 1: Multiple Choice Questions
What is the domain of the function f(x) = 1 / (x - 2)?
🤔 Note: The domain is all real numbers except where the denominator equals zero.
Answer: (−∞, 2) ∪ (2, ∞)What is the range of the function f(x) = x^2 + 3?
🤔 Note: The range is all real numbers greater than or equal to the minimum value.
Answer: [3, ∞)What is the domain of the function f(x) = |x|?
🤔 Note: The domain is all real numbers unless there is a restriction.
Answer: (−∞, ∞)
Section 2: Short Answer Questions
- Find the domain of the function f(x) = 2x / (x + 1).
Answer: (−∞, −1) ∪ (−1, ∞)
- Find the range of the function f(x) = x^2 - 4.
Answer: [−4, ∞)
Section 3: Word Problems
- A company produces a product where the cost is given by the function C(x) = 2x + 5, where x is the number of units produced. What is the domain of this function?
Answer: (0, ∞)
- A ball is thrown upward from the ground with an initial velocity of 20 feet per second. The height of the ball is given by the function h(t) = -16t^2 + 20t, where t is the time in seconds. What is the range of this function?
Answer: [0, 25]
Section 4: Graphing Questions
- Graph the function f(x) = |x - 2| and identify its domain and range.
Answer: Domain: (−∞, ∞), Range: [0, ∞)
- Graph the function f(x) = x^2 - 2 and identify its domain and range.
Answer: Domain: (−∞, ∞), Range: [−2, ∞)
Now that we’ve worked through these examples, let’s summarize the key points.
Functions have domains and ranges that can be determined based on their type and restrictions. By understanding these concepts, you’ll be able to analyze and graph functions with ease.
What is the difference between domain and range?
+The domain is the set of all possible input values for which the function is defined, while the range is the set of all possible output values.
How do I find the domain of a function?
+The domain depends on the type of function and its restrictions. For example, the domain of a rational function is all real numbers except where the denominator equals zero.
How do I find the range of a function?
+The range depends on the type of function and its restrictions. For example, the range of a quadratic function is all real numbers greater than or equal to the minimum value or less than or equal to the maximum value.



