5 Essential Domain and Range Rules
Understanding Domain and Range in Mathematics
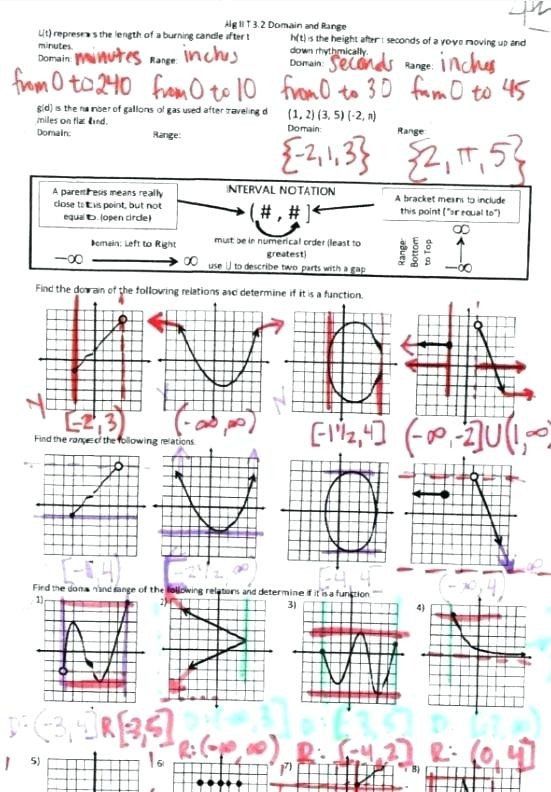
In mathematics, the domain and range of a function are two fundamental concepts that help define the behavior of the function. The domain refers to the set of all possible input values for which the function is defined, while the range refers to the set of all possible output values that the function can produce. Understanding these concepts is crucial for working with functions and solving problems in algebra, calculus, and other areas of mathematics.
Rule 1: Domain and Range of a Constant Function
A constant function is a function that always returns the same output value, regardless of the input value. For example, the function f(x) = 5 is a constant function because it always returns the output value 5, regardless of the input value x. The domain of a constant function is all real numbers, because any input value can be plugged into the function without causing division by zero or other errors. The range of a constant function is a single output value, in this case, 5.
🔥 Note: The domain of a constant function is always all real numbers, while the range is a single output value.
Rule 2: Domain and Range of a Linear Function
A linear function is a function of the form f(x) = mx + b, where m and b are constants. The domain of a linear function is all real numbers, because any input value can be plugged into the function without causing division by zero or other errors. The range of a linear function depends on the slope (m) and the y-intercept (b). If the slope is positive, the range is all real numbers greater than or equal to the y-intercept. If the slope is negative, the range is all real numbers less than or equal to the y-intercept.
Table: Domain and Range of Linear Functions
| Slope (m) | Domain | Range |
|---|---|---|
| m > 0 | All real numbers | All real numbers ≥ b |
| m < 0 | All real numbers | All real numbers ≤ b |
Rule 3: Domain and Range of a Quadratic Function
A quadratic function is a function of the form f(x) = ax^2 + bx + c, where a, b, and c are constants. The domain of a quadratic function is all real numbers, because any input value can be plugged into the function without causing division by zero or other errors. The range of a quadratic function depends on the leading coefficient (a) and the vertex of the parabola. If the leading coefficient is positive, the range is all real numbers greater than or equal to the y-coordinate of the vertex. If the leading coefficient is negative, the range is all real numbers less than or equal to the y-coordinate of the vertex.
Rule 4: Domain and Range of a Rational Function
A rational function is a function of the form f(x) = p(x)/q(x), where p(x) and q(x) are polynomials. The domain of a rational function is all real numbers except for the values that make the denominator zero. The range of a rational function depends on the degrees of the numerator and denominator. If the degree of the numerator is less than the degree of the denominator, the range is all real numbers except for the value 0. If the degree of the numerator is greater than or equal to the degree of the denominator, the range is all real numbers.
🔥 Note: The domain of a rational function is all real numbers except for the values that make the denominator zero.
Rule 5: Domain and Range of a Radical Function
A radical function is a function of the form f(x) = √(ax + b), where a and b are constants. The domain of a radical function is all real numbers greater than or equal to the value that makes the expression inside the square root zero. The range of a radical function is all real numbers greater than or equal to zero.
Table: Domain and Range of Radical Functions
| Radical Function | Domain | Range |
|---|---|---|
| f(x) = √(ax + b) | x ≥ -b/a | f(x) ≥ 0 |
Understanding the domain and range of different types of functions is essential for working with functions and solving problems in mathematics. By applying these rules, you can determine the domain and range of a function and identify any restrictions or limitations.
In conclusion, understanding the domain and range of functions is crucial for working with functions and solving problems in mathematics. By applying the rules outlined above, you can determine the domain and range of different types of functions and identify any restrictions or limitations.
What is the domain of a constant function?
+The domain of a constant function is all real numbers.
What is the range of a linear function?
+The range of a linear function depends on the slope (m) and the y-intercept (b). If the slope is positive, the range is all real numbers greater than or equal to the y-intercept. If the slope is negative, the range is all real numbers less than or equal to the y-intercept.
What is the domain of a rational function?
+The domain of a rational function is all real numbers except for the values that make the denominator zero.
Related Terms:
- Domain and Range Answer Key
- Domain and Range Worksheet 1
- Domain and Range Worksheet 2