Master Domain and Range with 5 Essential Interval Tips
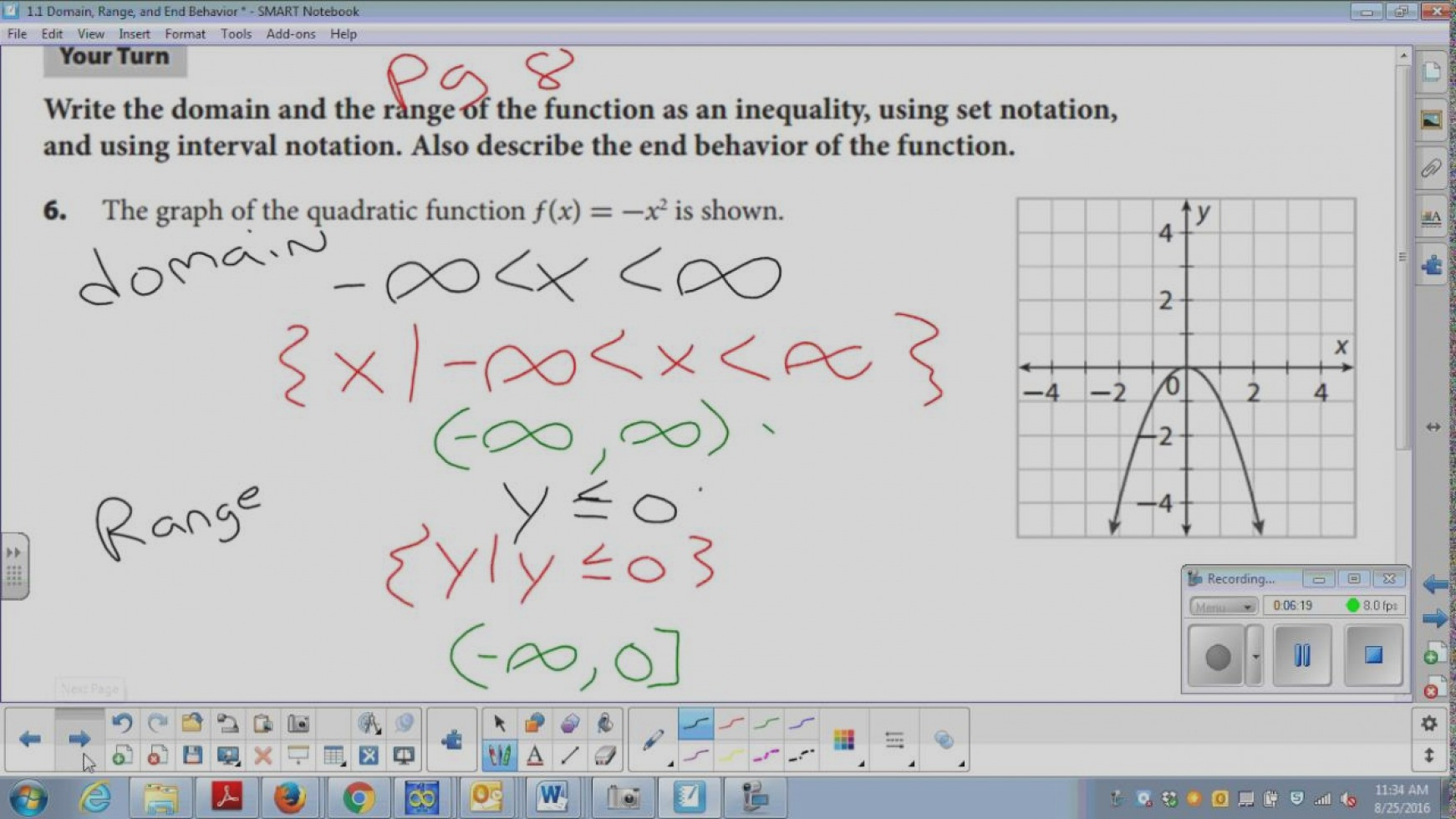
Understanding domain and range is crucial in mathematics, particularly in algebra and calculus. These concepts help you determine the possible input and output values of a function, ensuring you can solve problems accurately. Mastering domain and range requires practice, but with the right strategies, you can become proficient in no time. In this article, we’ll explore five essential interval tips to help you conquer domain and range.
What are Domain and Range?
Before we dive into the interval tips, let’s quickly review what domain and range mean:
- Domain: The set of all possible input values (x-values) for which a function is defined. In other words, it’s the set of values that you can plug into the function without causing any division by zero or taking the square root of a negative number.
- Range: The set of all possible output values (y-values) that a function can produce. It’s the set of values that the function can output.
Interval Notation
To represent domain and range, we use interval notation. Interval notation is a way of writing a set of numbers using brackets and parentheses. Here’s a quick rundown of the different types of intervals:
- Closed interval: a, b
- Open interval: (a, b) (excludes both a and b)
- Half-open interval: a, b) or (a, b
- Infinite interval: (a, ∞) or (-∞, b) (extends to infinity)
5 Essential Interval Tips for Mastering Domain and Range
Now that you know the basics, let’s move on to the five essential interval tips to help you master domain and range:
Tip 1: Identify the Type of Function
When dealing with domain and range, it’s essential to identify the type of function you’re working with. Different functions have different rules for determining domain and range.
- Polynomial functions: Domain is all real numbers, and range depends on the degree of the polynomial.
- Rational functions: Domain excludes values that make the denominator zero, and range depends on the type of rational function.
- Radical functions: Domain excludes values that make the radicand negative, and range depends on the type of radical function.
Tip 2: Use a Number Line to Visualize Intervals
Visualizing intervals on a number line can help you understand domain and range better. Draw a number line and mark the critical points (e.g., zeros, vertical asymptotes). Then, use the number line to determine the intervals that make up the domain and range.
Tip 3: Look for Restrictions in the Function
When finding the domain, look for restrictions in the function, such as:
- Zeros: Division by zero is undefined, so exclude values that make the denominator zero.
- Negative radicands: The square root of a negative number is undefined, so exclude values that make the radicand negative.
- Vertical asymptotes: These indicate values that are excluded from the domain.
Tip 4: Consider the Degree of the Polynomial
When finding the range of a polynomial function, consider the degree of the polynomial:
- Even degree: Range is all real numbers (or a subset of real numbers).
- Odd degree: Range is all real numbers (or a subset of real numbers), but the function may have a minimum or maximum value.
Tip 5: Check for Absolute Value and Square Root Functions
Absolute value and square root functions have specific rules for determining domain and range:
- Absolute value functions: Domain is all real numbers, but range is non-negative.
- Square root functions: Domain excludes negative values, and range is non-negative.
📝 Note: When dealing with absolute value and square root functions, make sure to consider the restrictions on the domain and range.
Conclusion
Mastering domain and range requires practice and a solid understanding of interval notation. By following these five essential interval tips, you’ll be well on your way to becoming a pro at determining domain and range. Remember to identify the type of function, use a number line to visualize intervals, look for restrictions, consider the degree of the polynomial, and check for absolute value and square root functions. With time and practice, you’ll become proficient in domain and range, and you’ll be able to tackle even the toughest math problems.
What is the difference between domain and range?
+Domain refers to the set of all possible input values (x-values) for which a function is defined, while range refers to the set of all possible output values (y-values) that a function can produce.
How do I determine the domain of a function?
+To determine the domain of a function, identify the type of function, look for restrictions, and use a number line to visualize intervals. Consider the degree of the polynomial and check for absolute value and square root functions.
What is interval notation?
+Interval notation is a way of writing a set of numbers using brackets and parentheses. It can be used to represent domain and range.
Related Terms:
- Interval notation practice