Cylinders Cones Spheres Volume Worksheet
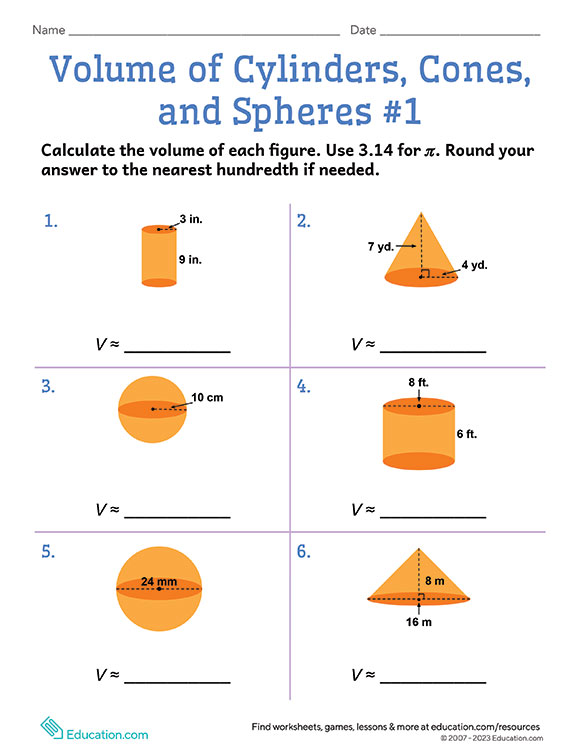
Mastering 3D Shapes: A Comprehensive Guide to Calculating Volumes of Cylinders, Cones, and Spheres
When it comes to three-dimensional geometry, understanding how to calculate the volumes of various shapes is crucial. In this article, we’ll delve into the world of cylinders, cones, and spheres, exploring their formulas, examples, and applications. Whether you’re a student, teacher, or simply a math enthusiast, this guide will help you grasp the concepts and become proficient in calculating the volumes of these fundamental 3D shapes.
Volume of a Cylinder
A cylinder is a three-dimensional shape with two parallel and circular bases connected by a curved lateral surface. To calculate the volume of a cylinder, you’ll need to know its radius ® and height (h).
Formula: V = πr²h
Where:
- V = volume of the cylinder
- π (pi) = approximately 3.14159
- r = radius of the cylinder
- h = height of the cylinder
Example:
Find the volume of a cylinder with a radius of 4 cm and a height of 10 cm.
V = π(4)²(10) = 3.14159 × 16 × 10 = 502.6552 cubic centimeters (or 502.66 cm³)
Volume of a Cone
A cone is a three-dimensional shape with a circular base and a vertex (apex) that tapers to a point. To calculate the volume of a cone, you’ll need to know its radius ® and height (h).
Formula: V = (1⁄3)πr²h
Where:
- V = volume of the cone
- π (pi) = approximately 3.14159
- r = radius of the cone
- h = height of the cone
Example:
Find the volume of a cone with a radius of 3 cm and a height of 8 cm.
V = (1⁄3)π(3)²(8) = (1⁄3) × 3.14159 × 9 × 8 = 75.398 cubic centimeters (or 75.40 cm³)
Volume of a Sphere
A sphere is a three-dimensional shape that is perfectly symmetrical about its center. To calculate the volume of a sphere, you’ll need to know its radius ®.
Formula: V = (4⁄3)πr³
Where:
- V = volume of the sphere
- π (pi) = approximately 3.14159
- r = radius of the sphere
Example:
Find the volume of a sphere with a radius of 5 cm.
V = (4⁄3)π(5)³ = (4⁄3) × 3.14159 × 125 = 523.5988 cubic centimeters (or 523.60 cm³)
Real-World Applications
Calculating the volumes of cylinders, cones, and spheres has numerous real-world applications, including:
- Engineering: Designing pipes, tubes, and containers requires accurate volume calculations to ensure proper functionality and efficiency.
- Architecture: Understanding the volumes of various shapes is crucial for designing buildings, bridges, and other structures.
- Science: Volume calculations are essential in various scientific fields, such as physics, chemistry, and biology, to analyze and understand complex phenomena.
Common Mistakes and Tips
When working with volume calculations, it’s essential to avoid common mistakes, such as:
- Incorrect unit conversions: Ensure that all measurements are in the same units to avoid errors.
- Rounding errors: Be cautious when rounding values, as this can lead to significant errors in calculations.
To improve your skills, try the following:
- Practice, practice, practice: The more you practice calculating volumes, the more comfortable you’ll become with the formulas and concepts.
- Use visual aids: Draw diagrams and visualize the shapes to better understand their properties and relationships.
📝 Note: Double-check your calculations and units to ensure accuracy.
Now that you’ve mastered the art of calculating volumes of cylinders, cones, and spheres, you’re ready to tackle more complex challenges in the world of 3D geometry.
What is the formula for the volume of a cylinder?
+V = πr²h, where V is the volume, π is approximately 3.14159, r is the radius, and h is the height.
How do I calculate the volume of a cone?
+V = (1⁄3)πr²h, where V is the volume, π is approximately 3.14159, r is the radius, and h is the height.
What is the formula for the volume of a sphere?
+V = (4⁄3)πr³, where V is the volume, π is approximately 3.14159, and r is the radius.



