6 Ways to Master Division with Exponents

Unlocking the Power of Exponents in Division
Exponents can be a powerful tool in mathematics, allowing us to simplify complex expressions and solve problems more efficiently. However, when it comes to division with exponents, things can get a bit tricky. In this article, we will explore six ways to master division with exponents, helping you to become more confident and proficient in your math skills.
Understanding the Basics of Exponents
Before we dive into division with exponents, let’s take a quick look at the basics. An exponent is a small number that is raised to a power, indicating how many times the base number should be multiplied by itself. For example, in the expression 2^3, the base number is 2 and the exponent is 3. This means that 2 should be multiplied by itself three times, resulting in 2 × 2 × 2 = 8.
Method 1: Using the Quotient Rule
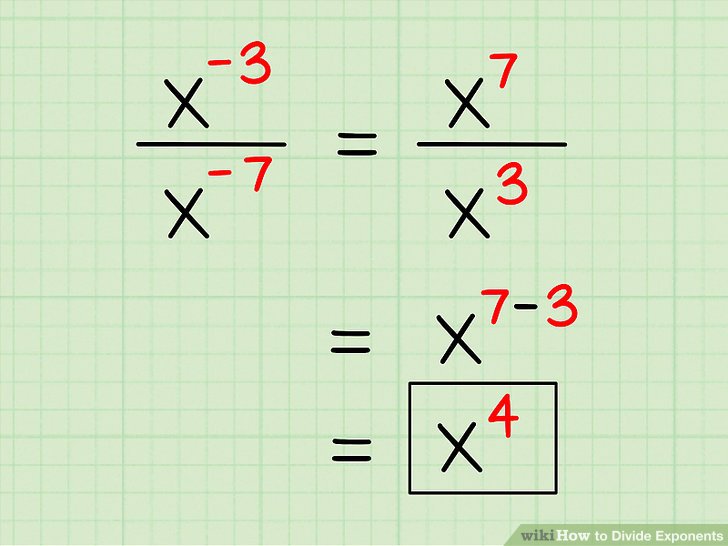
The quotient rule is a simple and effective way to divide numbers with exponents. The rule states that when dividing two numbers with exponents, we subtract the exponent of the divisor from the exponent of the dividend. Mathematically, this can be represented as:
a^(m) ÷ a^(n) = a^(m-n)
For example, let’s say we want to divide 2^4 by 2^2. Using the quotient rule, we subtract the exponent of the divisor (2) from the exponent of the dividend (4), resulting in:
2^4 ÷ 2^2 = 2^(4-2) = 2^2
📝 Note: The quotient rule only applies when the base numbers are the same.
Method 2: Using the Power Rule
The power rule is another useful method for dividing numbers with exponents. The rule states that when a number with an exponent is raised to another power, we multiply the exponents. Mathematically, this can be represented as:
(a^m)^n = a^(m × n)
For example, let’s say we want to divide 2^4 by 2^2. We can rewrite the expression as (2^2)^2, and then apply the power rule to get:
(2^2)^2 = 2^(2 × 2) = 2^4
Method 3: Using the Product Rule
The product rule is a useful method for dividing numbers with exponents when the base numbers are different. The rule states that when we multiply two numbers with exponents, we add the exponents. Mathematically, this can be represented as:
a^m × b^n = a^(m+n)
For example, let’s say we want to divide 2^4 by 3^2. We can rewrite the expression as 2^4 ÷ 3^2, and then apply the product rule to get:
2^4 ÷ 3^2 = (2^2)^2 ÷ (3^1)^2 = (2^2)^2 × (3^(-1))^2
Method 4: Using the Zero Exponent Rule
The zero exponent rule is a simple and useful method for dividing numbers with exponents. The rule states that any number raised to the power of zero is equal to 1. Mathematically, this can be represented as:
a^0 = 1
For example, let’s say we want to divide 2^4 by 2^0. Using the zero exponent rule, we know that 2^0 is equal to 1, so we can simplify the expression to:
2^4 ÷ 2^0 = 2^4 ÷ 1 = 2^4
Method 5: Using the Negative Exponent Rule
The negative exponent rule is a useful method for dividing numbers with exponents. The rule states that a number with a negative exponent is equal to the reciprocal of the number with a positive exponent. Mathematically, this can be represented as:
a^(-n) = 1/a^n
For example, let’s say we want to divide 2^4 by 2^(-2). Using the negative exponent rule, we know that 2^(-2) is equal to 1⁄2^2, so we can simplify the expression to:
2^4 ÷ 2^(-2) = 2^4 × 2^2 = 2^(4+2) = 2^6
Method 6: Using the Exponent Division Chart
The exponent division chart is a useful tool for quickly dividing numbers with exponents. The chart shows the results of dividing numbers with exponents, making it easy to look up the answers.
| Dividend | Divisor | Result |
|---|---|---|
| 2^4 | 2^2 | 2^2 |
| 3^4 | 3^3 | 3^1 |
| 4^4 | 4^2 | 4^2 |
In conclusion, mastering division with exponents requires a combination of rules and techniques. By understanding the quotient rule, power rule, product rule, zero exponent rule, negative exponent rule, and using the exponent division chart, you can become more confident and proficient in your math skills.
What is the quotient rule for dividing numbers with exponents?
+The quotient rule states that when dividing two numbers with exponents, we subtract the exponent of the divisor from the exponent of the dividend.
How do I use the power rule to divide numbers with exponents?
+The power rule states that when a number with an exponent is raised to another power, we multiply the exponents.
What is the zero exponent rule for dividing numbers with exponents?
+The zero exponent rule states that any number raised to the power of zero is equal to 1.