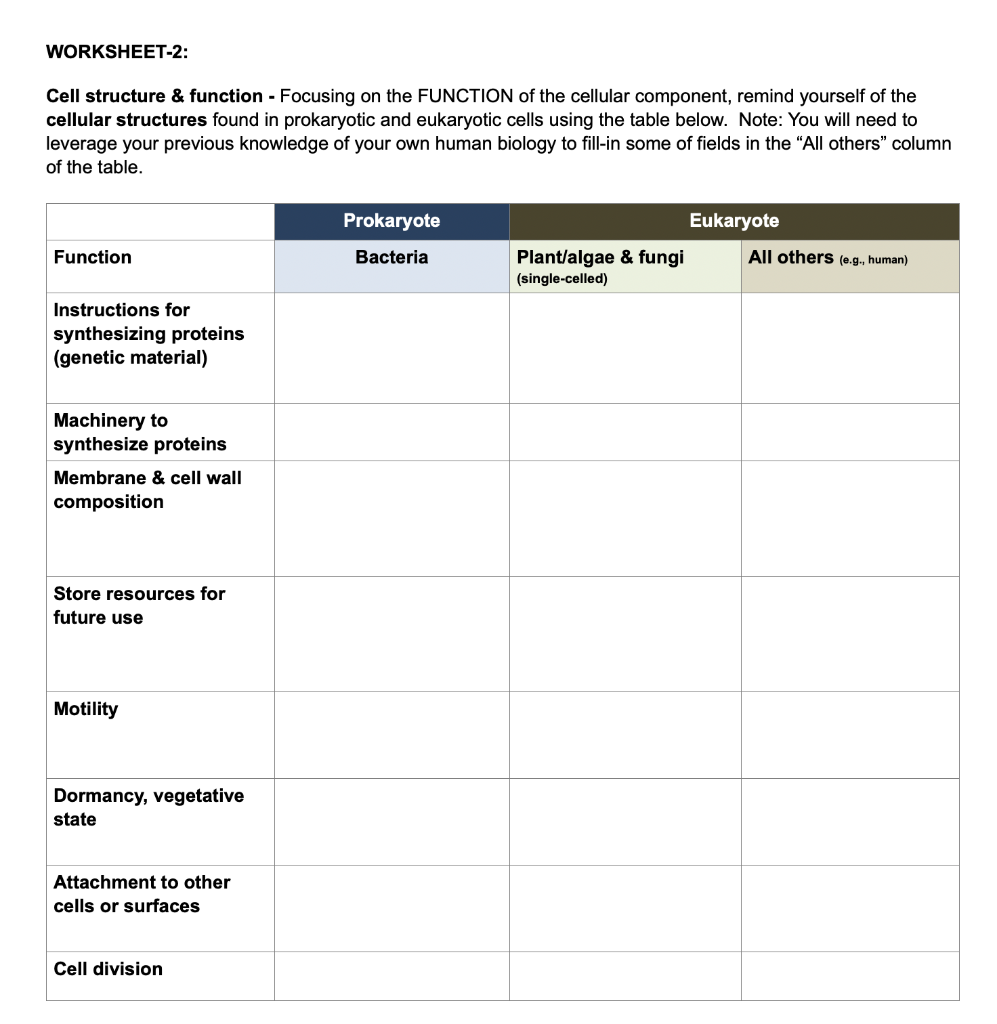
Coordinate Plane Worksheet for Math Success
Mastering the Coordinate Plane for Math Success
The coordinate plane is a fundamental concept in mathematics, used to graph points, lines, and shapes. It’s a crucial tool for problem-solving and critical thinking. In this article, we’ll explore the basics of the coordinate plane, its importance, and provide a comprehensive worksheet to help you master this essential math concept.
Understanding the Coordinate Plane
The coordinate plane is a two-dimensional grid system consisting of two axes: the x-axis (horizontal) and the y-axis (vertical). The point where the two axes intersect is called the origin, denoted as (0, 0). Each point on the plane is represented by a pair of coordinates (x, y), where x is the horizontal distance from the origin and y is the vertical distance.
Quadrants and Axes
The coordinate plane is divided into four quadrants:
- Quadrant I (upper right): (+, +)
- Quadrant II (upper left): (-, +)
- Quadrant III (lower left): (-, -)
- Quadrant IV (lower right): (+, -)
The x-axis and y-axis are used to measure distances and directions. The x-axis is divided into positive and negative values, while the y-axis is also divided into positive and negative values.
Plotting Points on the Coordinate Plane
To plot a point on the coordinate plane, follow these steps:
- Identify the x-coordinate (horizontal distance from the origin).
- Identify the y-coordinate (vertical distance from the origin).
- Move horizontally along the x-axis to the x-coordinate.
- Move vertically along the y-axis to the y-coordinate.
- Mark the point where the two coordinates intersect.
Example:
Plot the point (3, 4).
- Move 3 units to the right along the x-axis (positive x-value).
- Move 4 units up along the y-axis (positive y-value).
- Mark the point where the two coordinates intersect.
Coordinate Plane Worksheet
Now that you understand the basics of the coordinate plane, it’s time to practice! Complete the following worksheet to test your skills.
Section 1: Plotting Points
Plot the following points on the coordinate plane:

| Point | x-coordinate | y-coordinate |
|---|---|---|
| A | 2 | 5 |
| B | -3 | 2 |
| C | 0 | -4 |
| D | 1 | -2 |
| E | -2 | 0 |
Section 2: Identifying Quadrants
Determine the quadrant for each point:
| Point | x-coordinate | y-coordinate | Quadrant |
|---|---|---|---|
| F | 4 | 3 | |
| G | -2 | -5 | |
| H | 0 | 1 | |
| I | -1 | 2 | |
| J | 3 | -2 |
Section 3: Finding Distance and Midpoint
Find the distance between points A (2, 5) and B (-3, 2).
Find the midpoint of the line segment connecting points C (0, -4) and D (1, -2).
Solutions:
Section 1: Plotting Points
Plot the points on the coordinate plane:
| Point | x-coordinate | y-coordinate |
|---|---|---|
| A | 2 | 5 |
| B | -3 | 2 |
| C | 0 | -4 |
| D | 1 | -2 |
| E | -2 | 0 |
Section 2: Identifying Quadrants
Determine the quadrant for each point:
| Point | x-coordinate | y-coordinate | Quadrant |
|---|---|---|---|
| F | 4 | 3 | I |
| G | -2 | -5 | III |
| H | 0 | 1 | II |
| I | -1 | 2 | II |
| J | 3 | -2 | IV |
Section 3: Finding Distance and Midpoint
Find the distance between points A (2, 5) and B (-3, 2):
Distance = √((x2 - x1)^2 + (y2 - y1)^2) = √((-3 - 2)^2 + (2 - 5)^2) = √(25 + 9) = √34
Find the midpoint of the line segment connecting points C (0, -4) and D (1, -2):
Midpoint = ((x1 + x2) / 2, (y1 + y2) / 2) = ((0 + 1) / 2, (-4 + (-2)) / 2) = (0.5, -3)
Putting it all Together
The coordinate plane is a powerful tool for problem-solving and critical thinking. By mastering the basics of plotting points, identifying quadrants, and finding distances and midpoints, you’ll become proficient in using the coordinate plane to solve a wide range of math problems.
📝 Note: Practice regularly to reinforce your understanding of the coordinate plane. Try creating your own worksheets or using online resources to challenge yourself.
Mastering the coordinate plane takes time and practice. Stay committed, and you’ll become proficient in using this essential math concept to solve a wide range of problems.
What is the origin of the coordinate plane?
+The origin is the point where the x-axis and y-axis intersect, denoted as (0, 0).
How do I plot a point on the coordinate plane?
+To plot a point, identify the x-coordinate (horizontal distance from the origin) and y-coordinate (vertical distance from the origin). Move horizontally along the x-axis to the x-coordinate and vertically along the y-axis to the y-coordinate. Mark the point where the two coordinates intersect.
What is the formula for finding the distance between two points?
+The formula for finding the distance between two points is: Distance = √((x2 - x1)^2 + (y2 - y1)^2)