6 Ways to Master Constant of Proportionality
Understanding the Constant of Proportionality
The constant of proportionality is a fundamental concept in mathematics that describes the relationship between two quantities that are directly proportional. It is a constant value that represents the ratio of the two quantities, and it is essential in solving problems involving proportional relationships. In this blog post, we will explore six ways to master the constant of proportionality.
1. Identifying Proportional Relationships
To master the constant of proportionality, you need to be able to identify proportional relationships between two quantities. This involves recognizing that the ratio of the two quantities remains constant, even when the values of the quantities change. For example, if the cost of a certain number of items is directly proportional to the number of items, then the cost per item will remain constant.
📝 Note: Look for keywords such as "directly proportional," "in proportion," or "constant ratio" to identify proportional relationships.
2. Writing Proportional Equations
Once you have identified a proportional relationship, you can write an equation to represent it. A proportional equation takes the form y = kx, where y is the dependent variable, x is the independent variable, and k is the constant of proportionality. For example, if the cost of x items is 15, and the cost of 2x items is 30, you can write the equation C = 15x/2, where C is the cost and x is the number of items.
| Number of Items | Cost |
|---|---|
| x | $15 |
| 2x | $30 |
3. Solving Proportional Equations
To solve a proportional equation, you need to isolate the constant of proportionality (k). You can do this by dividing both sides of the equation by x. For example, if you have the equation C = 15x/2, you can divide both sides by x to get C/x = 15⁄2. This simplifies to k = 15⁄2.
4. Using the Constant of Proportionality to Solve Problems
The constant of proportionality can be used to solve problems involving proportional relationships. For example, if you know that the cost of 5 items is 75, and you want to find the cost of 10 items, you can use the constant of proportionality to solve the problem. If the cost per item is 15, then the cost of 10 items will be 10 x 15 = 150.
📝 Note: Use the constant of proportionality to solve problems involving proportional relationships, but make sure to check your units carefully.
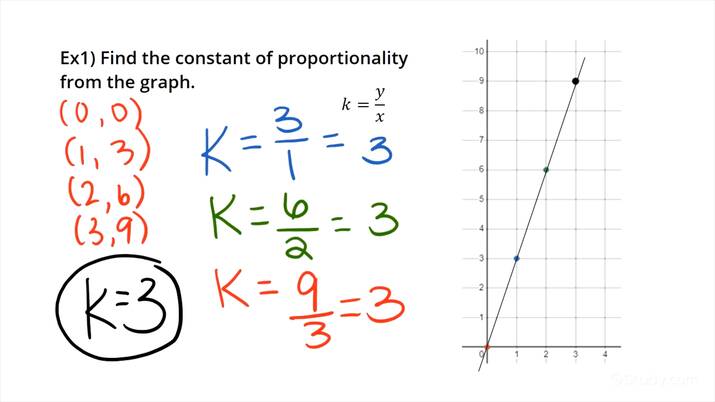
5. Graphing Proportional Relationships
Proportional relationships can be graphed on a coordinate plane. The graph of a proportional relationship is a straight line that passes through the origin. The slope of the line represents the constant of proportionality. For example, if the equation of a proportional relationship is y = 2x, then the slope of the line is 2.
6. Real-World Applications of the Constant of Proportionality
The constant of proportionality has many real-world applications. For example, it is used in physics to describe the relationship between force and acceleration, in economics to describe the relationship between price and demand, and in computer science to describe the relationship between input and output.
To summarize, the constant of proportionality is a fundamental concept in mathematics that describes the relationship between two quantities that are directly proportional. Mastering the constant of proportionality involves identifying proportional relationships, writing proportional equations, solving proportional equations, using the constant of proportionality to solve problems, graphing proportional relationships, and applying the concept to real-world problems.
What is the constant of proportionality?
+The constant of proportionality is a constant value that represents the ratio of two quantities that are directly proportional.
How do you write a proportional equation?
+A proportional equation takes the form y = kx, where y is the dependent variable, x is the independent variable, and k is the constant of proportionality.
What are some real-world applications of the constant of proportionality?
+The constant of proportionality has many real-world applications, including physics, economics, and computer science.



