Composite Volume Problems Made Easy
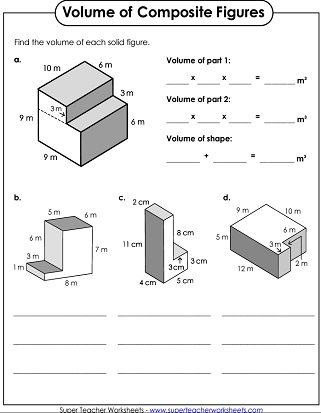
Introduction to Composite Volume Problems
Composite volume problems involve finding the volume of a shape that is composed of multiple simpler shapes. These types of problems can be challenging, but with the right approach, they can be made easy. In this article, we will break down the steps to solve composite volume problems and provide examples to help you understand the concept better.
Step 1: Break Down the Shape
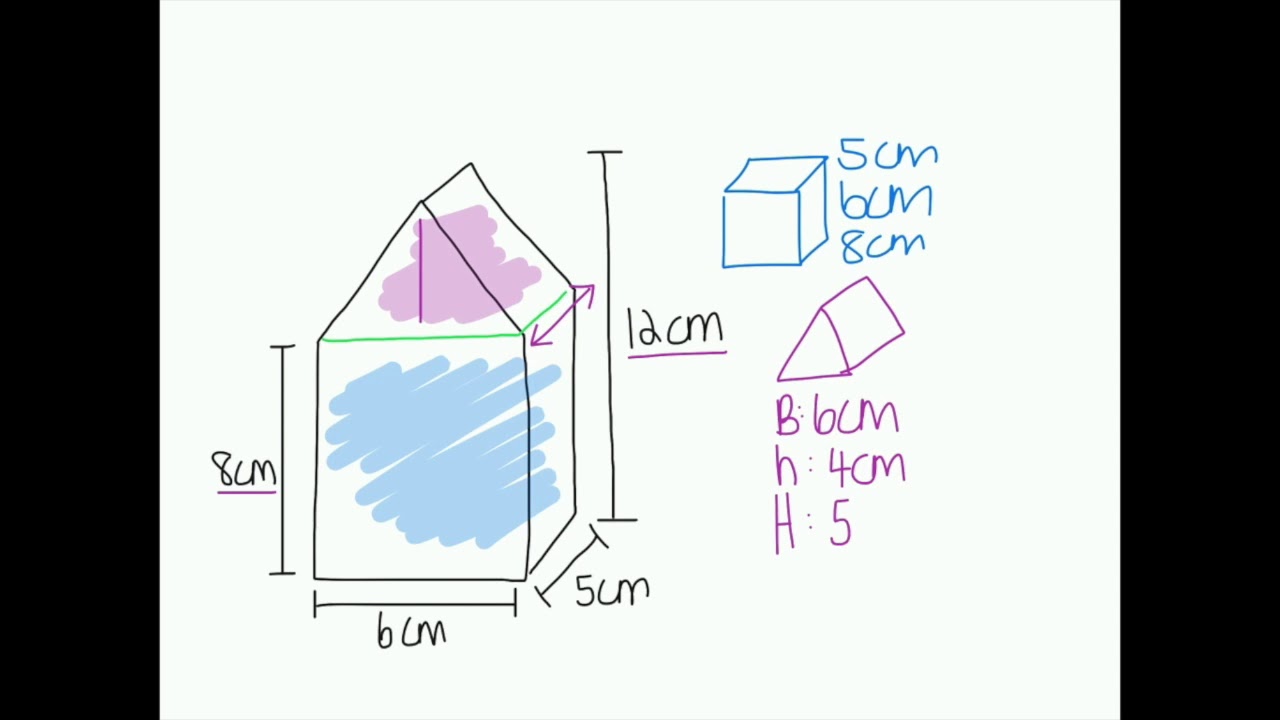
The first step in solving composite volume problems is to break down the shape into its individual components. This can be done by identifying the different shapes that make up the composite shape. For example, if we have a rectangular prism with a cylindrical hole, we can break it down into a rectangular prism and a cylinder.
Example:
Find the volume of a rectangular prism with a cylindrical hole. The rectangular prism has dimensions 6 cm x 4 cm x 2 cm, and the cylindrical hole has a radius of 1 cm and a height of 2 cm.
Step 2: Find the Volume of Each Component
Once we have broken down the shape into its individual components, we can find the volume of each component separately. The formula for the volume of a rectangular prism is length x width x height, and the formula for the volume of a cylinder is π x radius^2 x height.
Example (continued):
The volume of the rectangular prism is 6 cm x 4 cm x 2 cm = 48 cm^3.
The volume of the cylindrical hole is π x (1 cm)^2 x 2 cm = 2π cm^3.
Step 3: Subtract the Volume of the Hole
To find the volume of the composite shape, we need to subtract the volume of the hole from the volume of the rectangular prism.
Example (continued):
The volume of the composite shape is 48 cm^3 - 2π cm^3 = 48 cm^3 - 6.28 cm^3 = 41.72 cm^3.
Step 4: Check Your Units
It is essential to check your units to ensure that they are consistent throughout the problem. In this case, the units are cubic centimeters (cm^3).
Table of Formulas:
| Shape | Volume Formula |
|---|---|
| Rectangular Prism | Length x Width x Height |
| Cylinder | π x Radius^2 x Height |
Additional Tips and Tricks
- Always break down the shape into its individual components.
- Use the correct formula for the volume of each component.
- Check your units to ensure they are consistent throughout the problem.
- Practice, practice, practice!
🤔 Note: It is essential to practice solving composite volume problems to become proficient in breaking down complex shapes into simpler components.
Real-World Applications
Composite volume problems have numerous real-world applications, such as:
- Architecture: designing buildings with complex shapes
- Engineering: designing machines with multiple components
- Physics: calculating the volume of complex objects
Conclusion
Composite volume problems can be challenging, but by breaking down the shape into its individual components, finding the volume of each component, and subtracting the volume of the hole, we can make these problems easy. Remember to check your units and practice, practice, practice!
What is the formula for the volume of a rectangular prism?
+The formula for the volume of a rectangular prism is length x width x height.
What is the formula for the volume of a cylinder?
+The formula for the volume of a cylinder is π x radius^2 x height.
Why is it essential to check units in composite volume problems?
+It is essential to check units to ensure they are consistent throughout the problem to avoid errors and obtain accurate results.
Related Terms:
- Composite volume Worksheet pdf
- Composite volume worksheet with answers