5 Ways to Master Completing the Square

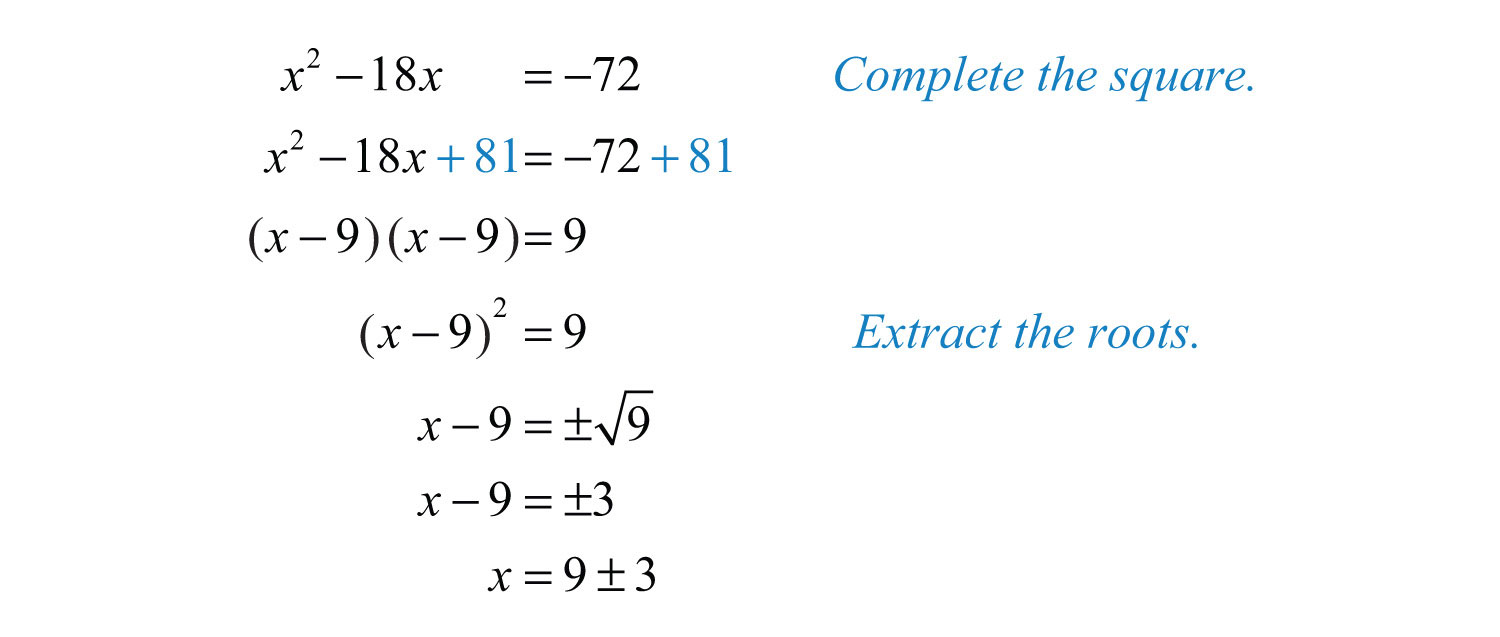
Unlocking the Power of Completing the Square

Completing the square is a fundamental technique in algebra that can help you solve quadratic equations and manipulate quadratic expressions. While it may seem daunting at first, mastering this technique can open up a world of possibilities for solving equations and graphing quadratic functions. In this article, we’ll explore five ways to master completing the square, making it easier for you to tackle even the most challenging quadratic problems.

Understanding the Basics

Before we dive into the five ways to master completing the square, let’s quickly review the basics. Completing the square involves manipulating a quadratic expression into a perfect square trinomial, which can then be easily factored or solved. The general form of a quadratic expression is:

ax^2 + bx + c

To complete the square, we need to create a perfect square trinomial by adding and subtracting a constant term.

Method 1: The Standard Method

The standard method of completing the square involves adding and subtracting a constant term to create a perfect square trinomial. Here’s how it works:

• Start with a quadratic expression in the form ax^2 + bx + c.
• Move the constant term to the right-hand side of the equation.
• Take half of the coefficient of the x-term, square it, and add it to both sides of the equation.
• Factor the perfect square trinomial on the left-hand side of the equation.

For example, let’s complete the square for the quadratic expression x^2 + 6x + 8:

x^2 + 6x + 8 = (x + 3)^2 - 1

📝 Note: Remember to move the constant term to the right-hand side of the equation before completing the square.

Method 2: Using the Formula

If you’re short on time or prefer a more straightforward approach, you can use the formula to complete the square:

(x + b/2a)^2 - (b^2 - 4ac)/4a

Where a, b, and c are the coefficients of the quadratic expression.

For example, let’s use the formula to complete the square for the quadratic expression x^2 + 4x + 3:

(x + 2)^2 - 1

📝 Note: Make sure to plug in the correct values for a, b, and c when using the formula.

Method 3: Graphical Approach

Visual learners may prefer the graphical approach to completing the square. This method involves graphing the quadratic function and using the vertex form to identify the perfect square trinomial.

• Graph the quadratic function using a graphing calculator or software.
• Identify the vertex of the parabola.
• Write the quadratic function in vertex form: a(x - h)^2 + k.
• Expand the vertex form to obtain the perfect square trinomial.

For example, let’s graph the quadratic function f(x) = x^2 + 2x + 1:

The vertex of the parabola is (-1, 0), so we can write the function in vertex form:

f(x) = (x + 1)^2 - 1

Method 4: Using Algebraic Manipulation

This method involves using algebraic manipulation to create a perfect square trinomial. Here’s how it works:

• Start with a quadratic expression in the form ax^2 + bx + c.
• Factor out the leading coefficient: a(x^2 + bx/a + c/a).
• Add and subtract a constant term to create a perfect square trinomial.

For example, let’s use algebraic manipulation to complete the square for the quadratic expression 2x^2 + 4x + 1:

2(x^2 + 2x + 1) = 2(x + 1)^2 - 1

📝 Note: Be careful when factoring out the leading coefficient to avoid mistakes.

Method 5: Using Technology

Finally, you can use technology to complete the square. Many graphing calculators and computer algebra systems (CAS) have built-in functions to complete the square.

• Enter the quadratic expression into the calculator or CAS.
• Use the built-in function to complete the square.
• Simplify the result to obtain the perfect square trinomial.

For example, let’s use a graphing calculator to complete the square for the quadratic expression x^2 + 3x + 2:

(x + 1.5)^2 - 0.25

As you can see, there are many ways to master completing the square. Whether you prefer the standard method, using the formula, or relying on technology, the key is to practice and become comfortable with the technique.

In summary, mastering completing the square requires practice, patience, and persistence. By using one or more of the five methods outlined above, you’ll be well on your way to solving quadratic equations and graphing quadratic functions with ease.

Related Terms:

• Completing the square Worksheet answers
• Completing the square Worksheet TES
• Completing the square worksheet corbettmaths
• Completing the square method