Complementary and Supplementary Angles Math Worksheet
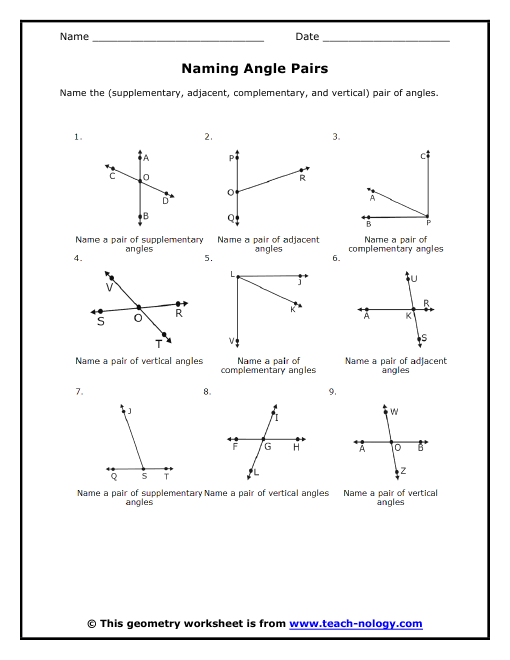
Understanding Complementary and Supplementary Angles
When it comes to angles, there are several key concepts to grasp in geometry. Two of these concepts are complementary and supplementary angles. In this article, we’ll delve into the world of angles, exploring what complementary and supplementary angles are, how to identify them, and provide a comprehensive math worksheet to help you practice.
What are Complementary Angles?
Complementary angles are two angles whose measures add up to 90 degrees. In other words, when you combine two complementary angles, they form a right angle (90 degrees). The measures of complementary angles can vary, but their sum is always 90 degrees.
Example: If one angle is 30 degrees, its complementary angle would be 60 degrees, since 30 + 60 = 90.
What are Supplementary Angles?
Supplementary angles are two angles whose measures add up to 180 degrees. When you combine two supplementary angles, they form a straight line (180 degrees). Like complementary angles, supplementary angles can have varying measures, but their sum is always 180 degrees.
Example: If one angle is 120 degrees, its supplementary angle would be 60 degrees, since 120 + 60 = 180.
Identifying Complementary and Supplementary Angles
To identify whether two angles are complementary or supplementary, you can use the following steps:
- Complementary Angles:
- Check if the sum of the two angles is 90 degrees.
- If the sum is 90 degrees, the angles are complementary.
- Supplementary Angles:
- Check if the sum of the two angles is 180 degrees.
- If the sum is 180 degrees, the angles are supplementary.
Math Worksheet: Complementary and Supplementary Angles
Here’s a comprehensive math worksheet to help you practice identifying complementary and supplementary angles:
Part 1: Multiple Choice
Choose the correct answer for each question:
- If angle A is 45 degrees, what is the measure of its complementary angle? a) 45 degrees b) 90 degrees c) 135 degrees d) 180 degrees
Answer: b) 90 degrees
- If angle B is 120 degrees, what is the measure of its supplementary angle? a) 60 degrees b) 90 degrees c) 120 degrees d) 180 degrees
Answer: a) 60 degrees
- If angle C is 30 degrees, what is the measure of its complementary angle? a) 30 degrees b) 60 degrees c) 90 degrees d) 120 degrees
Answer: b) 60 degrees
Part 2: Short Answer
- If angle D is 75 degrees, find the measure of its complementary angle.
Answer: 15 degrees (since 75 + 15 = 90)
- If angle E is 100 degrees, find the measure of its supplementary angle.
Answer: 80 degrees (since 100 + 80 = 180)
Part 3: Fill in the Blanks
- If angle F is 20 degrees, its complementary angle is __________ degrees.
Answer: 70 degrees (since 20 + 70 = 90)
- If angle G is 140 degrees, its supplementary angle is __________ degrees.
Answer: 40 degrees (since 140 + 40 = 180)
Part 4: Word Problems
- Tom is building a bookshelf, and he needs to cut two pieces of wood at complementary angles. If one piece is cut at 30 degrees, what angle should the other piece be cut at?
Answer: 60 degrees (since 30 + 60 = 90)
- Sarah is designing a room, and she wants to create a straight line with two walls. If one wall is built at 120 degrees, what angle should the other wall be built at?
Answer: 60 degrees (since 120 + 60 = 180)
Conclusion
Complementary and supplementary angles are fundamental concepts in geometry, and understanding them can help you solve a wide range of math problems. By practicing with this comprehensive math worksheet, you’ll become more confident in identifying these angles and applying them to real-world problems.
Remember, practice makes perfect! Take your time to work through the worksheet, and don’t hesitate to ask for help if you need it.
What is the difference between complementary and supplementary angles?
+
Complementary angles add up to 90 degrees, while supplementary angles add up to 180 degrees.
Can two angles be both complementary and supplementary?
+
No, two angles cannot be both complementary and supplementary. The sum of two complementary angles is 90 degrees, while the sum of two supplementary angles is 180 degrees.
How can I use complementary and supplementary angles in real-world problems?
+
Complementary and supplementary angles can be used in various real-world applications, such as architecture, design, and engineering. For example, when building a house, you might need to create a straight line with two walls, which would require supplementary angles. Similarly, when designing a room, you might want to create a right angle with two walls, which would require complementary angles.
Related Terms:
- Find missing angles worksheet pdf