5 Ways to Master Arc Length and Sector Area
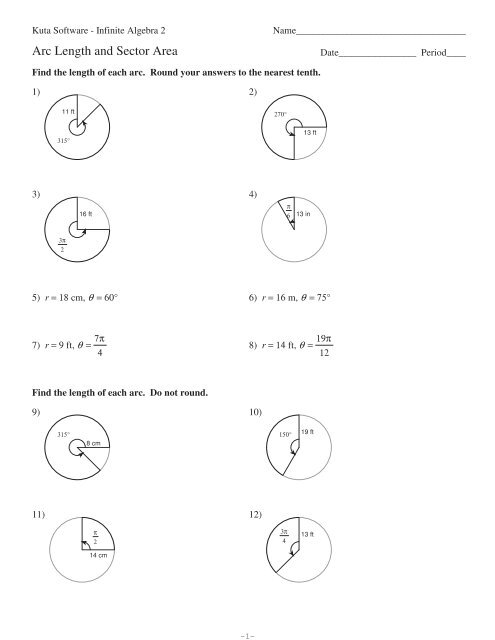
Understanding Arc Length and Sector Area
Arc length and sector area are two fundamental concepts in geometry and trigonometry that can be challenging to grasp for many students. However, with practice and a solid understanding of the underlying formulas, you can master these concepts and apply them to solve a wide range of problems. In this article, we will explore five ways to master arc length and sector area, along with examples and notes to help you along the way.
Way 1: Understanding the Formulas
To master arc length and sector area, it’s essential to start with the formulas. The arc length formula is:
Arc Length = (θ/360) × 2πr
where θ is the central angle in degrees, and r is the radius of the circle.
The sector area formula is:
Sector Area = (θ/360) × πr^2
where θ is the central angle in degrees, and r is the radius of the circle.
p class=“pro-note”>📝 Note: Make sure to convert the central angle to degrees if it’s given in radians.
Way 2: Visualizing the Concepts
Visualizing the concepts of arc length and sector area can help you understand them better. Imagine a pizza with a central angle of 60 degrees. The arc length would be the distance along the crust, while the sector area would be the area of the pizza slice.
You can also use online tools or graphing calculators to visualize the concepts and explore how different values of θ and r affect the arc length and sector area.
Way 3: Practicing with Examples
Practice is key to mastering arc length and sector area. Here are a few examples to get you started:
- Example 1: Find the arc length of a circle with a radius of 4 cm and a central angle of 90 degrees.
- Example 2: Find the sector area of a circle with a radius of 6 cm and a central angle of 120 degrees.
p class=“pro-note”>📝 Note: Make sure to show your work and explain your reasoning when solving problems.
Way 4: Using Real-World Applications
Arc length and sector area have many real-world applications, such as designing circular paths, determining the area of a sector-shaped plot of land, or calculating the length of a curve. Exploring these applications can help you see the relevance and importance of these concepts.
For example, imagine you’re designing a circular garden path with a radius of 10 meters and a central angle of 60 degrees. You can use the arc length formula to calculate the length of the path.
Way 5: Breaking Down Problems
Breaking down problems into smaller, manageable steps can help you solve them more efficiently. Here’s an example of how to break down a problem:
- Problem: Find the arc length and sector area of a circle with a radius of 8 cm and a central angle of 45 degrees.
- Step 1: Convert the central angle to radians (if necessary)
- Step 2: Plug in the values into the arc length formula
- Step 3: Simplify the expression and calculate the arc length
- Step 4: Plug in the values into the sector area formula
- Step 5: Simplify the expression and calculate the sector area
By breaking down problems into smaller steps, you can ensure that you’re using the correct formulas and calculations.
Wrapping Up
Mastering arc length and sector area requires practice, patience, and a solid understanding of the underlying formulas. By visualizing the concepts, practicing with examples, using real-world applications, and breaking down problems, you can become proficient in these concepts and apply them to solve a wide range of problems.
FAQ Section
What is the difference between arc length and sector area?
+
Arc length refers to the distance along a curve, while sector area refers to the area of a sector-shaped region.
How do I convert a central angle from degrees to radians?
+
To convert a central angle from degrees to radians, multiply the angle by π/180.
What are some real-world applications of arc length and sector area?
+
Arc length and sector area have many real-world applications, such as designing circular paths, determining the area of a sector-shaped plot of land, or calculating the length of a curve.
Related Terms:
- Arc length worksheet