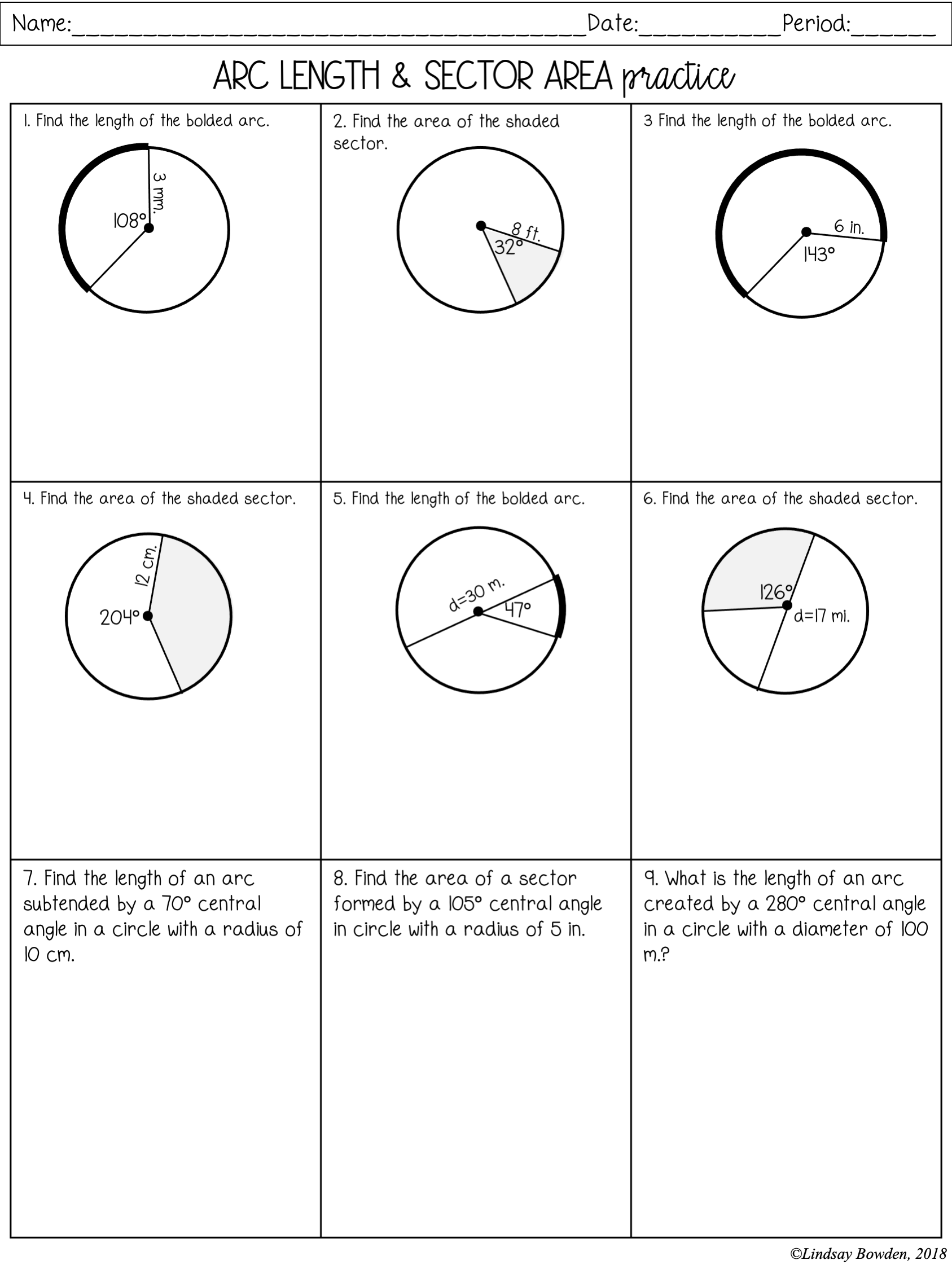
Complementary and Supplementary Angles Worksheet for Easy Learning

Mastering Complementary and Supplementary Angles: A Comprehensive Guide
In the realm of geometry, angles play a vital role in understanding various shapes and their properties. Two essential concepts that form the foundation of angle-related problems are complementary and supplementary angles. In this article, we will delve into the world of complementary and supplementary angles, exploring their definitions, properties, and applications through a worksheet-based approach.
What are Complementary Angles?
Complementary angles are two angles whose measures add up to 90 degrees. This means that if we have two angles, A and B, and their sum is 90 degrees, they are complementary. The relationship between complementary angles can be expressed as:
A + B = 90
📝 Note: Complementary angles do not have to be adjacent or form a linear pair.
What are Supplementary Angles?
Supplementary angles, on the other hand, are two angles whose measures add up to 180 degrees. This means that if we have two angles, A and B, and their sum is 180 degrees, they are supplementary. The relationship between supplementary angles can be expressed as:
A + B = 180
📝 Note: Supplementary angles do not have to be adjacent or form a linear pair.
Complementary and Supplementary Angles Worksheet
Now that we have a solid understanding of complementary and supplementary angles, let’s put our knowledge to the test with a worksheet. The following exercises will help you grasp the concepts better.
Exercise 1: Finding Complementary Angles
Find the complementary angle of the given angle:
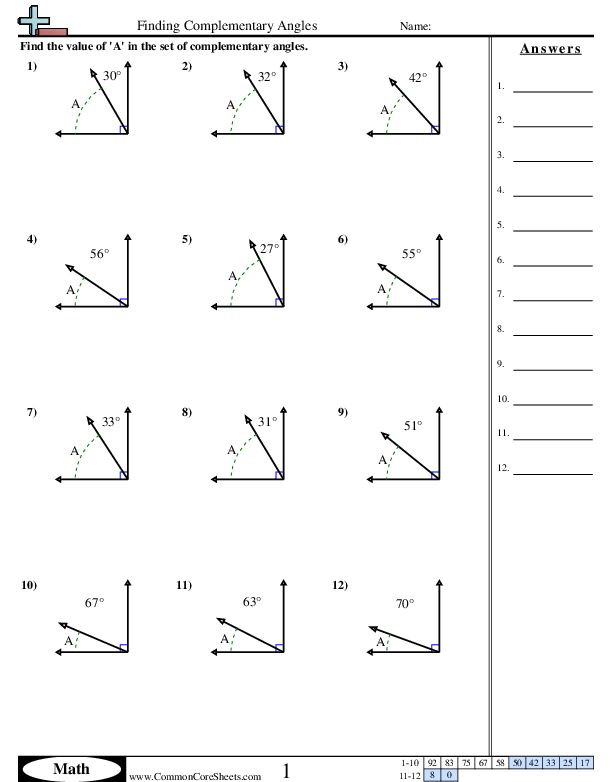
| Angle | Complementary Angle |
|---|---|
| 30° | ? |
| 60° | ? |
| 45° | ? |
Exercise 2: Finding Supplementary Angles
Find the supplementary angle of the given angle:
| Angle | Supplementary Angle |
|---|---|
| 120° | ? |
| 90° | ? |
| 150° | ? |
Exercise 3: Identifying Complementary and Supplementary Angles
Identify whether the given angles are complementary or supplementary:
| Angle 1 | Angle 2 | Relationship |
|---|---|---|
| 30° | 60° | ? |
| 120° | 60° | ? |
| 45° | 135° | ? |
Exercise 4: Solving Problems with Complementary and Supplementary Angles
Solve the following problems using complementary and supplementary angles:
- If two angles are complementary and one angle measures 40°, what is the measure of the other angle?
- If two angles are supplementary and one angle measures 75°, what is the measure of the other angle?
Exercise 5: Word Problems with Complementary and Supplementary Angles
Solve the following word problems using complementary and supplementary angles:
- In a right triangle, the acute angles are complementary. If one angle measures 30°, what is the measure of the other acute angle?
- In a triangle, the sum of two interior angles is 180°. If one angle measures 90°, what is the measure of the other interior angle?
Answers and Explanations
Exercise 1: Finding Complementary Angles
| Angle | Complementary Angle |
|---|---|
| 30° | 60° |
| 60° | 30° |
| 45° | 45° |
Exercise 2: Finding Supplementary Angles
| Angle | Supplementary Angle |
|---|---|
| 120° | 60° |
| 90° | 90° |
| 150° | 30° |
Exercise 3: Identifying Complementary and Supplementary Angles
| Angle 1 | Angle 2 | Relationship |
|---|---|---|
| 30° | 60° | Complementary |
| 120° | 60° | Supplementary |
| 45° | 135° | Supplementary |
Exercise 4: Solving Problems with Complementary and Supplementary Angles
- If two angles are complementary and one angle measures 40°, the other angle measures 50°.
- If two angles are supplementary and one angle measures 75°, the other angle measures 105°.
Exercise 5: Word Problems with Complementary and Supplementary Angles
- In a right triangle, the acute angles are complementary. If one angle measures 30°, the other acute angle measures 60°.
- In a triangle, the sum of two interior angles is 180°. If one angle measures 90°, the other interior angle measures 90°.
📝 Note: Make sure to check your answers and explanations to ensure a thorough understanding of the concepts.
In conclusion, mastering complementary and supplementary angles is crucial for solving various problems in geometry. By practicing with the worksheet provided, you have taken the first step towards becoming proficient in these concepts. Remember to always apply the relationships between complementary and supplementary angles to solve problems efficiently.
What is the difference between complementary and supplementary angles?
+Complementary angles are two angles whose measures add up to 90 degrees, while supplementary angles are two angles whose measures add up to 180 degrees.
Can complementary angles be adjacent?
+No, complementary angles do not have to be adjacent or form a linear pair.
How can I identify whether two angles are complementary or supplementary?
+You can identify whether two angles are complementary or supplementary by checking if their sum is 90 degrees (complementary) or 180 degrees (supplementary).