5 Ways to Compare Fractions with Models Easily
Understanding Fractions and Their Importance in Math
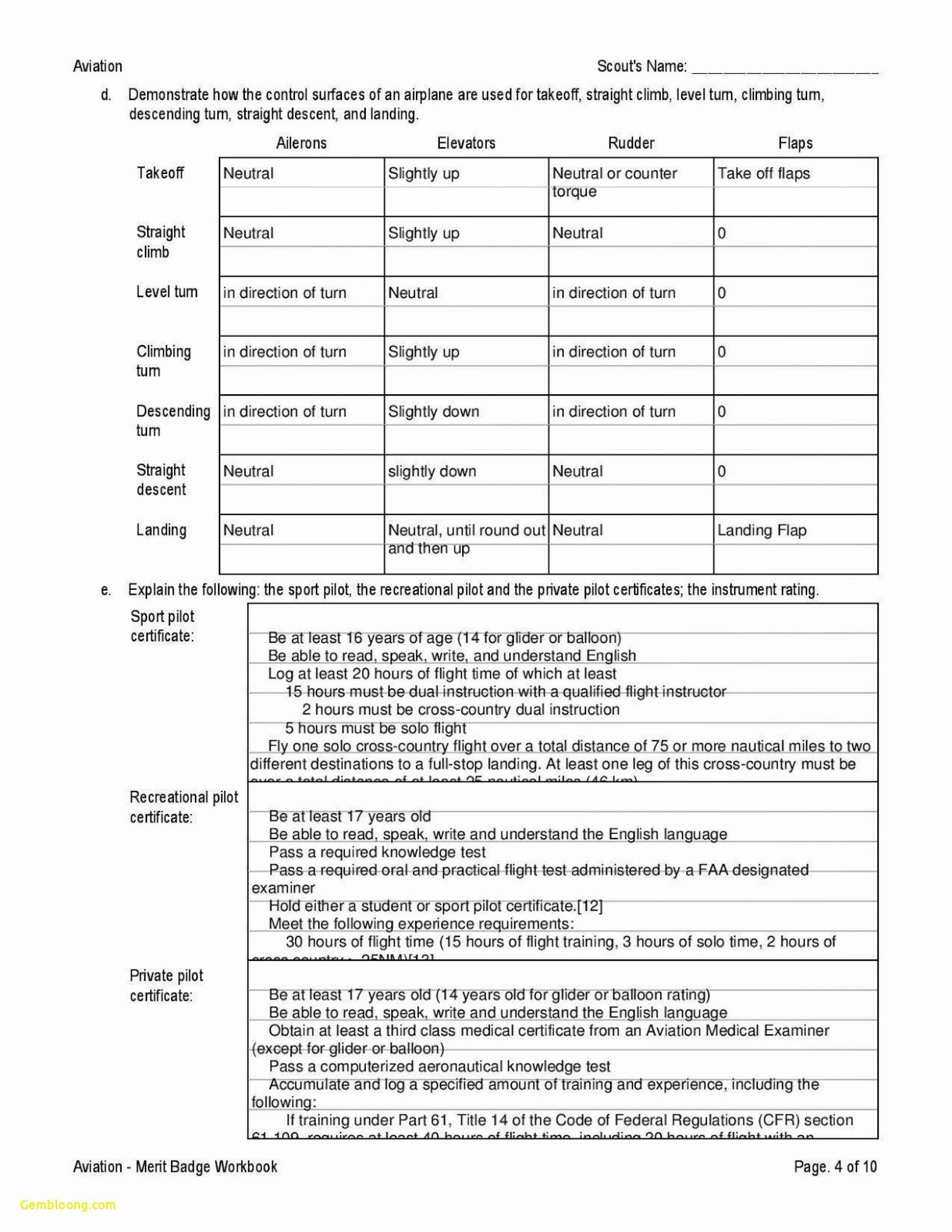
Fractions are a fundamental concept in mathematics, representing a part of a whole. They consist of a numerator (the top number) and a denominator (the bottom number), separated by a line. Fractions are essential in various mathematical operations, such as addition, subtraction, multiplication, and division. Comparing fractions is a crucial skill in math, and using models can make it easier and more visual.
Why Comparing Fractions is Important
Comparing fractions is a critical skill in math, as it helps students understand the relationships between different fractions. It enables them to determine which fraction is larger or smaller, and by how much. This skill is essential in various real-world applications, such as measuring ingredients for cooking, calculating distances, and comparing sizes.
Method 1: Using Number Lines
One way to compare fractions is by using number lines. A number line is a visual representation of numbers on a line, which can help students understand the relationships between different fractions. To compare fractions using a number line, follow these steps:
- Draw a number line with marks for whole numbers and fractions.
- Plot the fractions on the number line.
- Compare the positions of the fractions on the number line to determine which one is larger or smaller.
For example, to compare 1⁄2 and 3⁄4, plot both fractions on the number line. Since 3⁄4 is farther to the right, it is larger than 1⁄2.
📝 Note: Number lines can be drawn with different scales, depending on the fractions being compared.
Method 2: Using Fraction Strips
Fraction strips are another visual tool to compare fractions. They consist of strips of paper or other materials with different lengths, each representing a fraction. To compare fractions using fraction strips, follow these steps:
- Create fraction strips for each fraction being compared.
- Place the fraction strips side by side to compare their lengths.
- The longer strip represents the larger fraction.
For example, to compare 2⁄3 and 3⁄4, create fraction strips for each fraction. Since the 3⁄4 strip is longer, it is larger than 2⁄3.
📝 Note: Fraction strips can be made from paper, cardboard, or other materials.
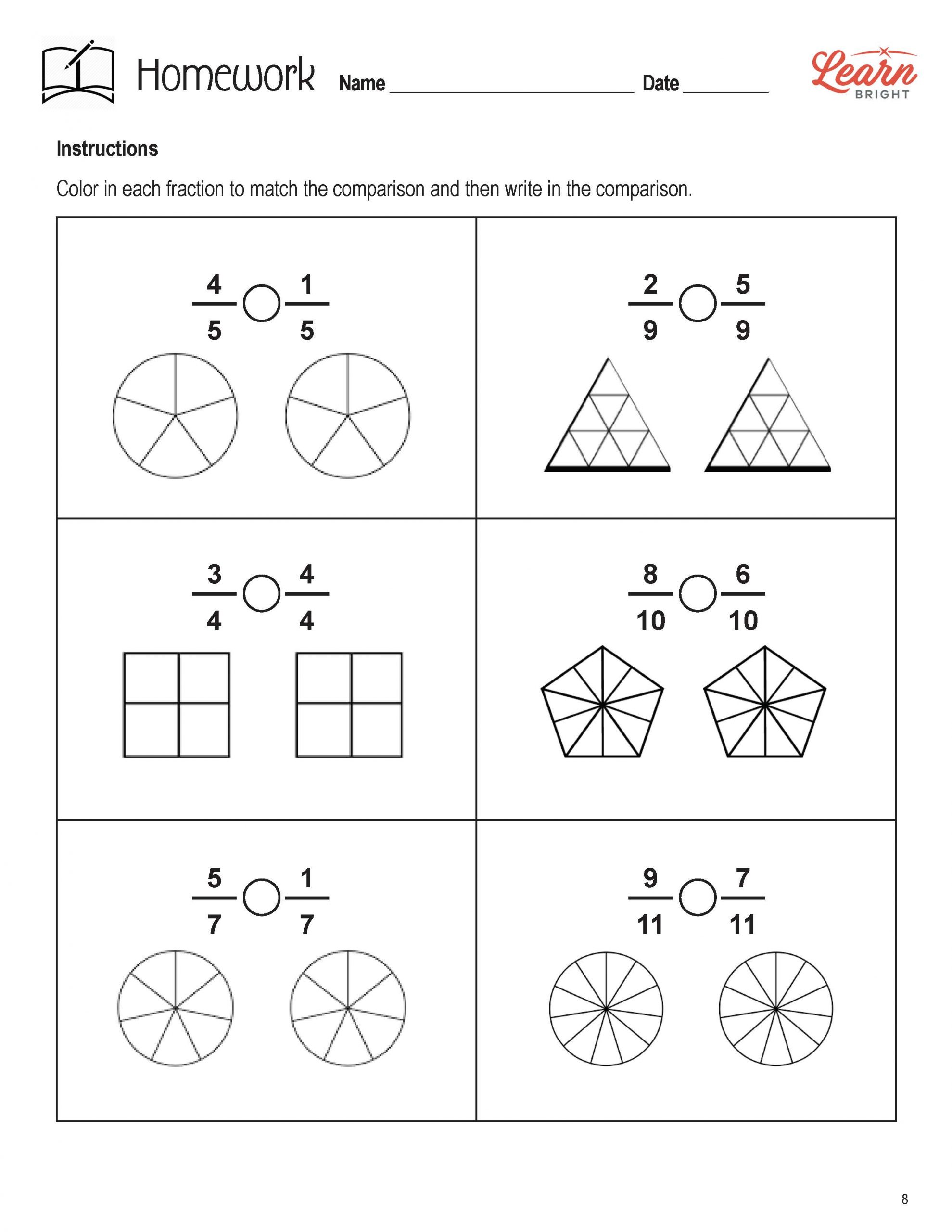
Method 3: Using Fraction Circles
Fraction circles are circular models that can be used to compare fractions. They consist of a circle divided into equal parts, each representing a fraction. To compare fractions using fraction circles, follow these steps:
- Draw a fraction circle for each fraction being compared.
- Shade the corresponding parts of each circle to represent the fractions.
- Compare the shaded areas to determine which fraction is larger or smaller.
For example, to compare 1⁄4 and 1⁄2, draw a fraction circle for each fraction. Shade one-quarter of the circle for 1⁄4 and one-half of the circle for 1⁄2. Since the shaded area for 1⁄2 is larger, it is greater than 1⁄4.
📝 Note: Fraction circles can be drawn with different sizes and colors.
Method 4: Using Real-World Objects
Real-world objects can be used to compare fractions in a more concrete way. For example, to compare 1⁄2 and 3⁄4, use a pizza or a cake. Divide the pizza or cake into equal parts, and shade or mark the corresponding parts to represent the fractions. Compare the shaded areas to determine which fraction is larger or smaller.
📝 Note: Real-world objects can make comparing fractions more engaging and meaningful.
Method 5: Using Technology
Technology, such as math apps and online tools, can also be used to compare fractions. These tools often provide interactive models and visual representations of fractions, making it easier for students to compare them. Some popular math apps for comparing fractions include Math Playground, Khan Academy, and IXL.
📝 Note: Technology can provide interactive and engaging ways to compare fractions.
Comparing fractions with models is an effective way to visualize and understand the relationships between different fractions. By using number lines, fraction strips, fraction circles, real-world objects, and technology, students can develop a deeper understanding of fractions and improve their math skills.
To summarize, comparing fractions with models involves using visual representations to understand the relationships between different fractions. The five methods discussed above provide a range of approaches to compare fractions, from using number lines and fraction strips to real-world objects and technology. By using these methods, students can develop a stronger understanding of fractions and improve their math skills.
What is the best way to compare fractions?
+The best way to compare fractions is by using visual models, such as number lines, fraction strips, and fraction circles.
Can I use real-world objects to compare fractions?
+Yes, real-world objects can be used to compare fractions in a more concrete way.
What are some popular math apps for comparing fractions?
+Some popular math apps for comparing fractions include Math Playground, Khan Academy, and IXL.