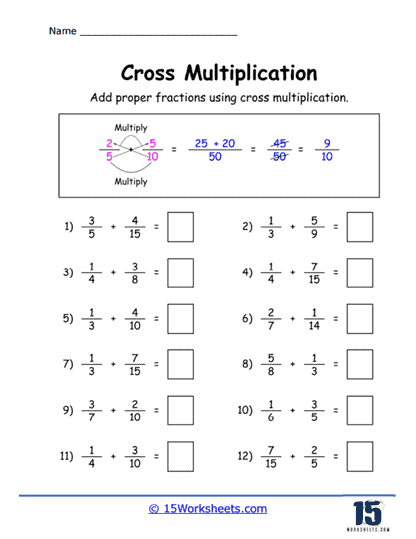
Comparing Fractions With Like Numerators Worksheet
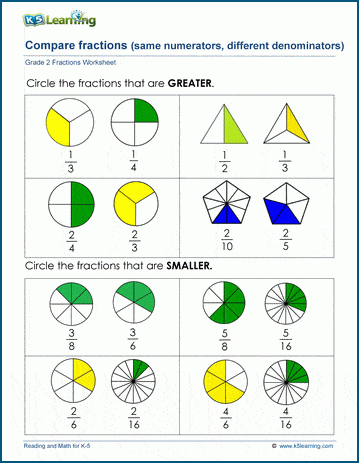
Comparing Fractions With Like Numerators: A Comprehensive Guide
When it comes to fractions, comparing them can be a bit tricky, especially when the numerators are the same. In this post, we’ll dive into the world of fractions with like numerators, explore what they are, and provide a step-by-step guide on how to compare them.
What Are Fractions With Like Numerators?
Fractions with like numerators are fractions that have the same numerator but different denominators. For example:
- 1⁄2 and 1⁄4
- 3⁄8 and 3⁄12
- 2⁄3 and 2⁄5
In each of these examples, the numerators are the same, but the denominators are different.
Why Compare Fractions With Like Numerators?
Comparing fractions with like numerators is an essential skill in mathematics, particularly in algebra and geometry. It helps you:
- Understand the relationship between fractions
- Determine which fraction is larger or smaller
- Simplify complex fractions
- Solve equations and inequalities
How to Compare Fractions With Like Numerators
Comparing fractions with like numerators is relatively straightforward. Here’s a step-by-step guide:
- Check the denominators: Since the numerators are the same, focus on the denominators. The fraction with the smaller denominator is the larger fraction.
- Compare the denominators: If the denominators are different, compare them. The fraction with the smaller denominator is the larger fraction.
- Use equivalent fractions: If the denominators are multiples of each other, use equivalent fractions to compare them.
Let’s use an example to illustrate this:
Compare 1⁄2 and 1⁄4
- Check the denominators: The denominators are 2 and 4.
- Compare the denominators: Since 2 is smaller than 4, 1⁄2 is larger than 1⁄4.
Therefore, 1⁄2 is greater than 1⁄4.
Examples and Exercises
Here are some examples and exercises to help you practice comparing fractions with like numerators:
- Compare 3⁄8 and 3⁄12
- Compare 2⁄3 and 2⁄5
- Compare 1⁄6 and 1⁄8
Take your time to work through these examples and exercises. Remember to check the denominators, compare them, and use equivalent fractions if necessary.
Notes
📝 Note: When comparing fractions with like numerators, make sure to focus on the denominators. The fraction with the smaller denominator is the larger fraction.
Table: Comparing Fractions With Like Numerators
| Fraction 1 | Fraction 2 | Comparison |
|---|---|---|
| 1/2 | 1/4 | 1/2 > 1/4 |
| 3/8 | 3/12 | 3/8 > 3/12 |
| 2/3 | 2/5 | 2/3 > 2/5 |
Conclusion
Comparing fractions with like numerators is a fundamental skill in mathematics. By focusing on the denominators and using equivalent fractions, you can determine which fraction is larger or smaller. Remember to practice regularly to become more comfortable with comparing fractions with like numerators.
What are fractions with like numerators?
+Fractions with like numerators are fractions that have the same numerator but different denominators.
Why compare fractions with like numerators?
+Comparing fractions with like numerators helps you understand the relationship between fractions, determine which fraction is larger or smaller, simplify complex fractions, and solve equations and inequalities.
How do I compare fractions with like numerators?
+Compare fractions with like numerators by checking the denominators, comparing them, and using equivalent fractions if necessary.
Related Terms:
- Comparing fractions with same denominator
- Comparing fractions Worksheet with answers
- Comparing fractions Worksheet grade 4