Compare Fractions Same Denominator Worksheet
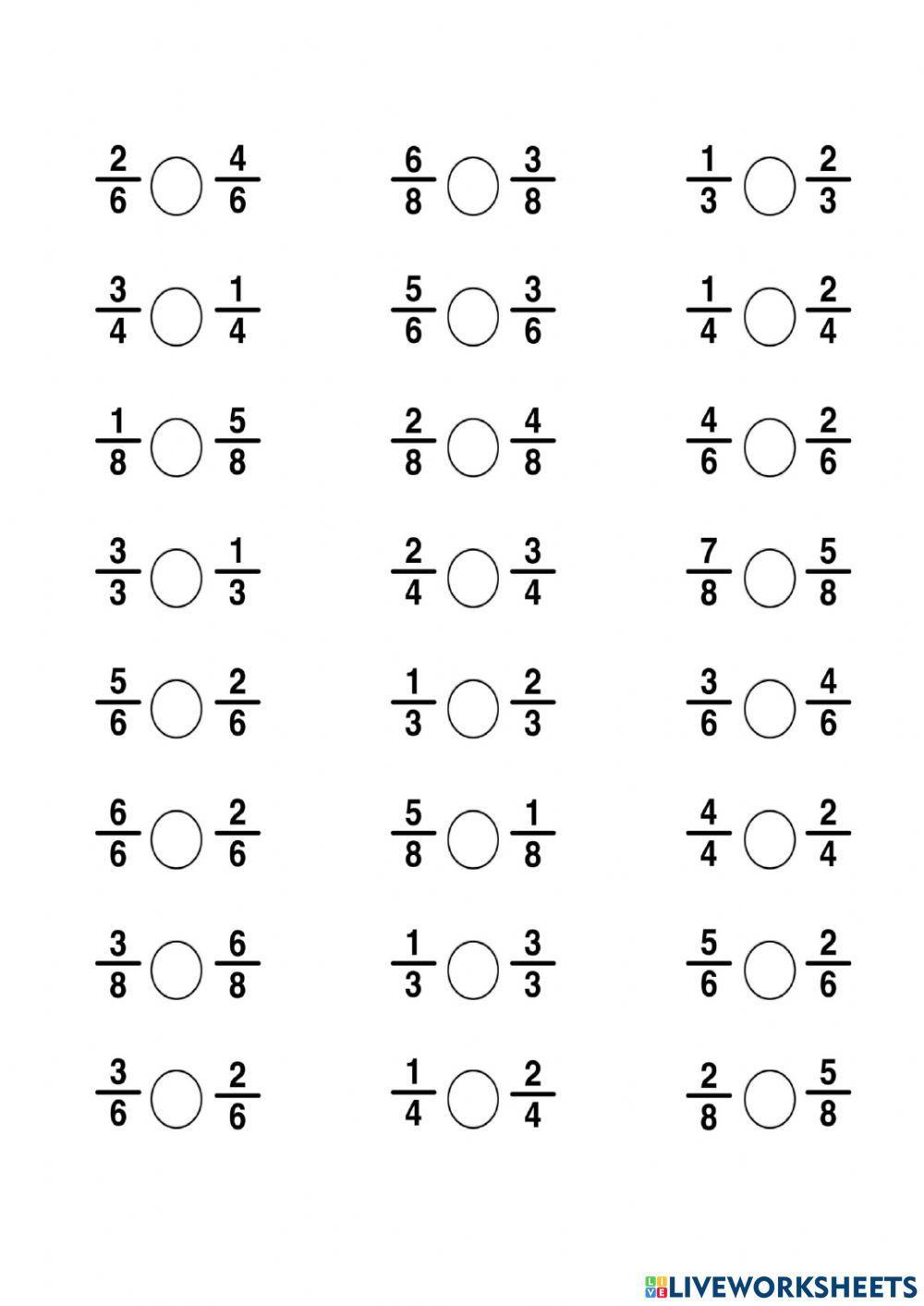
Comparing Fractions with the Same Denominator: A Comprehensive Guide
Fractions are a fundamental concept in mathematics, and comparing them is an essential skill for students to master. When fractions have the same denominator, it becomes easier to compare them. In this article, we will delve into the world of fractions with the same denominator, explore the concept, and provide a worksheet to help students practice.
Understanding Fractions with the Same Denominator
Fractions consist of a numerator (the top number) and a denominator (the bottom number). The denominator represents the total number of equal parts, while the numerator represents the number of parts we are interested in. When two fractions have the same denominator, it means they are divided into the same number of equal parts.
For example, consider the fractions 1⁄8 and 3⁄8. Both fractions have the same denominator, 8, which means they are divided into 8 equal parts. To compare these fractions, we need to look at the numerators. The fraction with the larger numerator (3) is greater than the fraction with the smaller numerator (1).
Comparing Fractions with the Same Denominator
To compare fractions with the same denominator, follow these steps:
- Step 1: Check if the denominators are the same. If they are not, you cannot compare the fractions using this method.
- Step 2: Compare the numerators. The fraction with the larger numerator is greater than the fraction with the smaller numerator.
- Step 3: Write the comparison symbol (<, >, or =) to indicate the relationship between the fractions.
Here are some examples:
- 2⁄6 and 5⁄6: Since the denominators are the same (6), we compare the numerators. 5 is greater than 2, so 5⁄6 > 2⁄6.
- 3⁄12 and 7⁄12: Again, the denominators are the same (12). 7 is greater than 3, so 7⁄12 > 3⁄12.
- 1⁄4 and 1⁄4: The numerators are the same (1), and the denominators are the same (4). Therefore, the fractions are equal (1⁄4 = 1⁄4).
Worksheet: Comparing Fractions with the Same Denominator
Now it’s time to practice! Complete the following worksheet to compare fractions with the same denominator.
| Fraction 1 | Fraction 2 | Comparison |
|---|---|---|
| 2⁄8 | 5⁄8 | |
| 3⁄12 | 9⁄12 | |
| 1⁄6 | 4⁄6 | |
| 7⁄10 | 3⁄10 | |
| 2⁄4 | 2⁄4 | |
| 9⁄16 | 13⁄16 | |
| 5⁄8 | 1⁄8 | |
| 6⁄12 | 8⁄12 |
Answer Key:
| Fraction 1 | Fraction 2 | Comparison |
|---|---|---|
| 2⁄8 | 5⁄8 | 2⁄8 < 5⁄8 |
| 3⁄12 | 9⁄12 | 3⁄12 < 9⁄12 |
| 1⁄6 | 4⁄6 | 1⁄6 < 4⁄6 |
| 7⁄10 | 3⁄10 | 7⁄10 > 3⁄10 |
| 2⁄4 | 2⁄4 | 2⁄4 = 2⁄4 |
| 9⁄16 | 13⁄16 | 9⁄16 < 13⁄16 |
| 5⁄8 | 1⁄8 | 5⁄8 > 1⁄8 |
| 6⁄12 | 8⁄12 | 6⁄12 < 8⁄12 |
🤔 Note: When comparing fractions with the same denominator, it's essential to remember that the larger numerator indicates the greater fraction.
Conclusion
Comparing fractions with the same denominator is a straightforward process that requires attention to the numerators. By following the steps outlined in this article and practicing with the worksheet, students can develop a solid understanding of this concept. Remember, fractions are an essential part of mathematics, and mastering them will open doors to more advanced mathematical concepts.
What is the main concept of comparing fractions with the same denominator?
+The main concept is to compare the numerators, as the denominators are the same. The fraction with the larger numerator is greater than the fraction with the smaller numerator.
How do I determine if two fractions have the same denominator?
+Check if the bottom numbers (denominators) are the same. If they are, you can compare the fractions using the steps outlined in this article.
Can I compare fractions with different denominators using this method?
+No, this method only applies to fractions with the same denominator. To compare fractions with different denominators, you need to use other methods, such as finding the least common multiple (LCM) or using equivalent fractions.