7 Ways to Master Common Denominator

Understanding the Concept of Common Denominator
The common denominator is a fundamental concept in mathematics, particularly in fractions and algebra. It is the least common multiple (LCM) of the denominators of two or more fractions. Mastering the common denominator is essential for adding, subtracting, multiplying, and dividing fractions. In this article, we will explore seven ways to master the common denominator.
1. Understanding the Concept of Least Common Multiple (LCM)
To find the common denominator, you need to calculate the LCM of the denominators. The LCM is the smallest number that is a multiple of both numbers. For example, the LCM of 4 and 6 is 12.
📝 Note: To calculate the LCM, list the multiples of each number and find the smallest common multiple.
2. Using the Prime Factorization Method
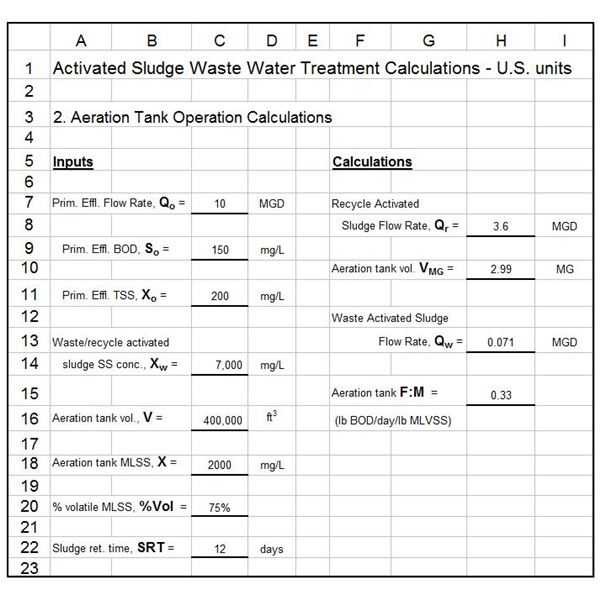
Another way to find the LCM is by using the prime factorization method. This involves breaking down each number into its prime factors and then multiplying the highest power of each prime factor.

| Number | Prime Factors |
|---|---|
| 4 | 2 × 2 |
| 6 | 2 × 3 |
📝 Note: Multiply the highest power of each prime factor to find the LCM. In this case, the LCM is 2 × 2 × 3 = 12.
3. Using the Listing Method
The listing method involves listing the multiples of each number and finding the smallest common multiple.
| Multiples of 4 | Multiples of 6 |
|---|---|
| 4, 8, 12, 16,... | 6, 12, 18, 24,... |
📝 Note: The smallest common multiple is 12.
4. Finding the Common Denominator of Two Fractions
To find the common denominator of two fractions, calculate the LCM of the denominators.
Example: Find the common denominator of 1⁄4 and 1⁄6.
📝 Note: Calculate the LCM of 4 and 6 to find the common denominator. The LCM is 12.
5. Adding and Subtracting Fractions with Different Denominators
To add or subtract fractions with different denominators, find the common denominator and convert each fraction to have the common denominator.
Example: Add 1⁄4 and 1⁄6.
📝 Note: Find the common denominator (12) and convert each fraction to have the common denominator: 3/12 + 2/12 = 5/12.
6. Multiplying and Dividing Fractions with Different Denominators
To multiply or divide fractions with different denominators, find the common denominator and convert each fraction to have the common denominator.
Example: Multiply 1⁄4 and 1⁄6.
📝 Note: Find the common denominator (12) and convert each fraction to have the common denominator: (3/12) × (2/12) = 6/144.
7. Practicing with Real-World Examples
Practicing with real-world examples will help you master the common denominator. Try solving problems involving fractions with different denominators.
Example: A recipe calls for 1⁄4 cup of flour and 1⁄6 cup of sugar. What is the total amount of ingredients needed?
📝 Note: Find the common denominator (12) and convert each fraction to have the common denominator: 3/12 + 2/12 = 5/12 cup.
In conclusion, mastering the common denominator is essential for working with fractions. By understanding the concept of LCM, using the prime factorization method, listing method, and practicing with real-world examples, you can become proficient in finding the common denominator.
What is the common denominator?
+The common denominator is the least common multiple (LCM) of the denominators of two or more fractions.
How do I find the common denominator?
+Calculate the LCM of the denominators using the prime factorization method or the listing method.
Why is mastering the common denominator important?
+Mastering the common denominator is essential for adding, subtracting, multiplying, and dividing fractions.
Related Terms:
- Common denominator Worksheet PDF
- Common denominator worksheets grade 5
- Free printable common denominator worksheets
- Least common denominator worksheet PDF
- Finding common denominators anchor chart
- Common denominator exercises