5 Ways to Calculate Triangle Area Easily
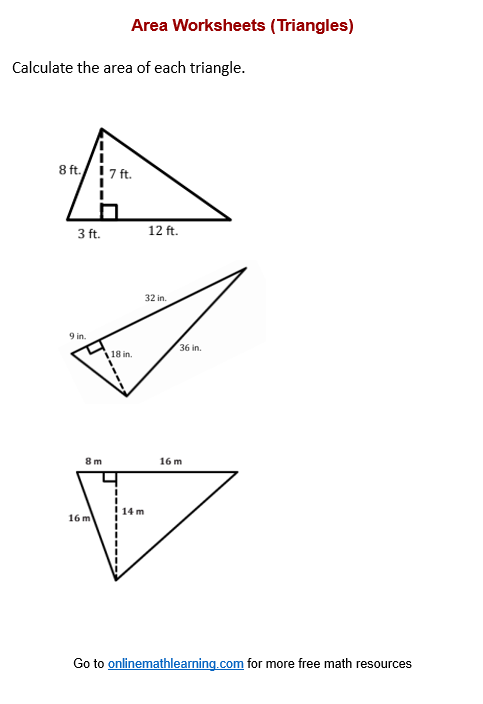
Understanding Triangle Area Calculations
Calculating the area of a triangle is a fundamental concept in geometry and trigonometry. It is essential in various fields, including engineering, architecture, and physics. There are several methods to calculate the area of a triangle, each with its own advantages and limitations. In this article, we will explore five common methods to calculate triangle area easily.
Method 1: Using the Formula (Base × Height) / 2
This is one of the most straightforward methods to calculate the area of a triangle. The formula is:
Area = (Base × Height) / 2
Where:
- Base is the length of one side of the triangle
- Height is the perpendicular distance from the base to the opposite vertex
This method requires knowing the base and height of the triangle. If you have a right triangle, you can easily find the height using the Pythagorean theorem.
📝 Note: This method is only applicable if you know the base and height of the triangle.
Method 2: Using Heron's Formula
Heron’s formula is a more complex method to calculate the area of a triangle, but it is useful when you know the lengths of all three sides. The formula is:
Area = √(s(s-a)(s-b)(s-c))
Where:
- s is the semi-perimeter of the triangle (s = (a + b + c) / 2)
- a, b, and c are the lengths of the three sides of the triangle
This method is useful when you know the lengths of all three sides, but not the height.
📝 Note: This method is more complex than the first method, but it is useful when you know the lengths of all three sides.
Method 3: Using the Law of Cosines
The law of cosines is a fundamental concept in trigonometry that relates the lengths of the sides of a triangle to the cosine of one of its angles. The formula is:
c² = a² + b² - 2ab cos©
Where:
- c is the length of the third side of the triangle
- a and b are the lengths of the other two sides
- C is the angle between sides a and b
This method requires knowing the lengths of two sides and the angle between them.
📝 Note: This method is useful when you know the lengths of two sides and the angle between them.
Method 4: Using the Shoelace Formula
The shoelace formula is a method to calculate the area of a polygon, including triangles. The formula is:
Area = (1⁄2) |x₁y₂ + x₂y₃ +… + xₙy₁ - y₁x₂ - y₂x₃ -… - yₙx₁|
Where:
- (x₁, y₁), (x₂, y₂),…, (xₙ, yₙ) are the coordinates of the vertices of the triangle
This method requires knowing the coordinates of the vertices of the triangle.
📝 Note: This method is useful when you know the coordinates of the vertices of the triangle.
Method 5: Using the Triangle Area Calculator
If you don’t want to calculate the area of a triangle manually, you can use an online triangle area calculator. These calculators are available on various websites and can be used for free.
📝 Note: Online calculators are useful when you need to calculate the area of a triangle quickly and accurately.
What is the most common method to calculate the area of a triangle?
+The most common method to calculate the area of a triangle is using the formula (Base × Height) / 2.
What is Heron's formula used for?
+Heron's formula is used to calculate the area of a triangle when you know the lengths of all three sides.
Can I use the law of cosines to calculate the area of a triangle?
+Yes, you can use the law of cosines to calculate the area of a triangle, but it requires knowing the lengths of two sides and the angle between them.
In conclusion, calculating the area of a triangle is a fundamental concept in geometry and trigonometry. There are several methods to calculate the area of a triangle, each with its own advantages and limitations. By understanding these methods, you can easily calculate the area of a triangle using the formula that best suits your needs.
Related Terms:
- The area of triangle
- Word problem area of triangle
- Area of compound shapes worksheet
- Area of square worksheet



