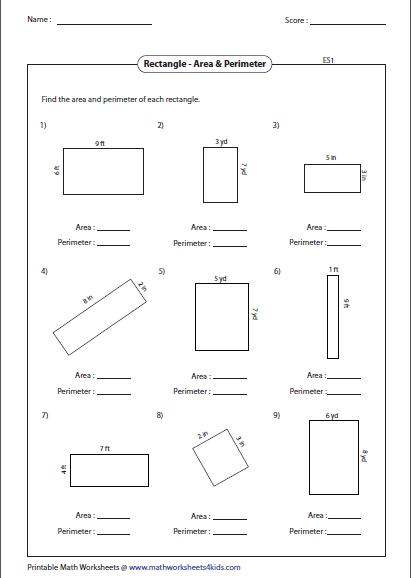
Rectangle Area and Perimeter Worksheet for Math Practice

Mastering Rectangle Area and Perimeter Calculations
Understanding the concepts of area and perimeter is crucial in mathematics, especially when dealing with geometric shapes like rectangles. A rectangle is a four-sided shape with opposite sides of equal length, making it a fundamental shape in various mathematical and real-world applications. In this article, we will delve into the formulas and calculations for the area and perimeter of rectangles, providing a comprehensive guide for students and educators.
Formulas for Rectangle Area and Perimeter
Before we proceed to practice problems, it’s essential to grasp the formulas for calculating the area and perimeter of a rectangle.
- Area of a Rectangle (A): A = length × width
- Perimeter of a Rectangle (P): P = 2 × (length + width)
These formulas are straightforward, but applying them to different problems can help solidify your understanding.
Practice Problems for Rectangle Area and Perimeter
Let’s move on to some practice problems to put your knowledge to the test. We’ll provide a mix of problems that involve finding the area, perimeter, or both.
Problem 1: Finding the Area of a Rectangle
A rectangle has a length of 8 cm and a width of 5 cm. What is its area?
Solution:
A = length × width A = 8 cm × 5 cm A = 40 cm²
Problem 2: Calculating the Perimeter of a Rectangle
A rectangle has a length of 10 cm and a width of 6 cm. What is its perimeter?
Solution:
P = 2 × (length + width) P = 2 × (10 cm + 6 cm) P = 2 × 16 cm P = 32 cm
Problem 3: Finding the Width of a Rectangle Given Its Area and Length
A rectangle has an area of 72 cm² and a length of 9 cm. What is its width?
Solution:
A = length × width 72 cm² = 9 cm × width width = 72 cm² ÷ 9 cm width = 8 cm
Problem 4: Finding the Length of a Rectangle Given Its Perimeter and Width
A rectangle has a perimeter of 36 cm and a width of 7 cm. What is its length?
Solution:
P = 2 × (length + width) 36 cm = 2 × (length + 7 cm) 18 cm = length + 7 cm length = 18 cm - 7 cm length = 11 cm
💡 Note: Make sure to check your units when solving these problems, as they should match the question's requirements.
Table of Rectangle Area and Perimeter Formulas
| Formula | Description |
|---|---|
| A = length × width | Area of a rectangle |
| P = 2 × (length + width) | Perimeter of a rectangle |
Mastering Rectangle Calculations: Tips and Tricks
- When solving problems, make sure to label your lengths and widths correctly to avoid confusion.
- Use the formulas as a guide, but also try to visualize the rectangle to ensure your calculations make sense.
- Practice, practice, practice! The more problems you solve, the more comfortable you’ll become with these formulas.
By following these tips and practicing with the provided problems, you’ll become proficient in calculating the area and perimeter of rectangles in no time.
Finding the area and perimeter of rectangles is a fundamental math skill that can be applied to various real-world situations. Whether you’re building a fence, designing a room, or simply solving math problems, mastering these calculations is essential. Remember to always check your units, label your variables correctly, and practice regularly to become a math pro!
What is the difference between the area and perimeter of a rectangle?
+The area of a rectangle refers to the amount of space inside the shape, while the perimeter refers to the distance around the shape.
How do I calculate the length of a rectangle if I know its width and perimeter?
+Use the perimeter formula (P = 2 × (length + width)) and rearrange it to solve for length: length = (P ÷ 2) - width.
What are some real-world applications of rectangle area and perimeter calculations?
+These calculations can be applied to building design, furniture making, gardening, and more. Any situation where you need to calculate the area or perimeter of a rectangular shape can benefit from these formulas.