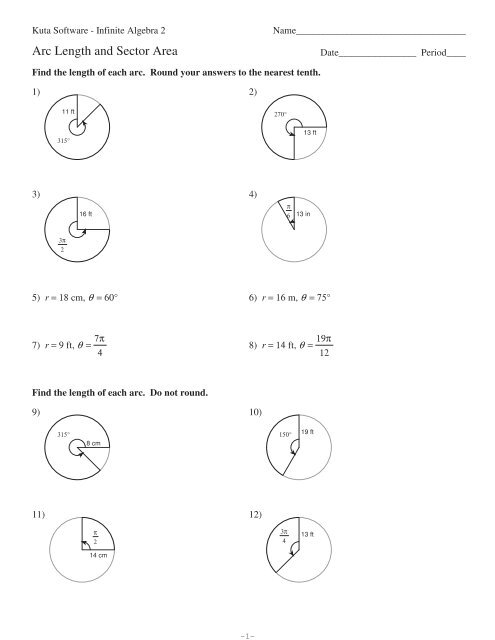
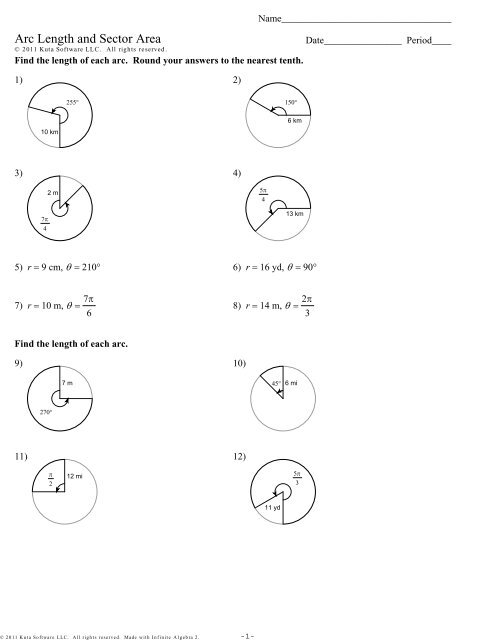
Arc Length And Sector Area Worksheet With Answers
Understanding Arc Length and Sector Area
When working with circles, it’s essential to understand the concepts of arc length and sector area. In this article, we’ll delve into the definitions, formulas, and examples of these concepts, along with a comprehensive worksheet to help you practice and reinforce your understanding.
What is Arc Length?
The arc length is the distance along a curve or a circular arc. In the context of a circle, it’s the length of the arc subtended by a central angle. The formula to calculate the arc length is:
Arc Length = (θ / 360) × 2πr
where:
- θ (theta) is the central angle in degrees
- r is the radius of the circle
For example, if the central angle is 60° and the radius is 4 cm, the arc length would be:
Arc Length = (60 / 360) × 2π(4) = 4π/3 cm
What is Sector Area?
A sector is a region of a circle bounded by two radii and an arc. The sector area is the area of this region. The formula to calculate the sector area is:
Sector Area = (θ / 360) × πr^2
where:
- θ (theta) is the central angle in degrees
- r is the radius of the circle
For example, if the central angle is 60° and the radius is 4 cm, the sector area would be:
Sector Area = (60 / 360) × π(4)^2 = 4π/3 cm^2
Worksheet
Here’s a worksheet with 10 questions to help you practice calculating arc length and sector area:
| # | Central Angle (θ) | Radius ® | Arc Length / Sector Area |
|---|---|---|---|
| 1 | 30° | 6 cm | Arc Length |
| 2 | 45° | 8 cm | Sector Area |
| 3 | 90° | 10 cm | Arc Length |
| 4 | 120° | 12 cm | Sector Area |
| 5 | 150° | 8 cm | Arc Length |
| 6 | 210° | 10 cm | Sector Area |
| 7 | 240° | 12 cm | Arc Length |
| 8 | 270° | 8 cm | Sector Area |
| 9 | 300° | 10 cm | Arc Length |
| 10 | 330° | 12 cm | Sector Area |
Answers
| # | Answer |
|---|---|
| 1 | Arc Length = π/2 cm |
| 2 | Sector Area = 8π/5 cm^2 |
| 3 | Arc Length = π cm |
| 4 | Sector Area = 12π/5 cm^2 |
| 5 | Arc Length = 2π/3 cm |
| 6 | Sector Area = 14π/5 cm^2 |
| 7 | Arc Length = 4π/5 cm |
| 8 | Sector Area = 8π/3 cm^2 |
| 9 | Arc Length = 5π/6 cm |
| 10 | Sector Area = 44π/15 cm^2 |
📝 Note: Make sure to show your work and use the formulas provided to calculate the arc length and sector area for each problem.
To reinforce your understanding, try to work out the problems on your own before checking the answers.
Conclusion
Understanding arc length and sector area is crucial in mathematics, particularly in geometry and trigonometry. By practicing with this worksheet, you’ll become more comfortable with the formulas and calculations involved. Remember to apply these concepts to real-world problems and explore their applications in various fields.
What is the difference between arc length and sector area?
+Arc length refers to the distance along a circular arc, while sector area refers to the area of a region bounded by two radii and an arc.
How do I calculate arc length?
+Use the formula: Arc Length = (θ / 360) × 2πr, where θ is the central angle in degrees and r is the radius of the circle.
What is the formula for sector area?
+Use the formula: Sector Area = (θ / 360) × πr^2, where θ is the central angle in degrees and r is the radius of the circle.