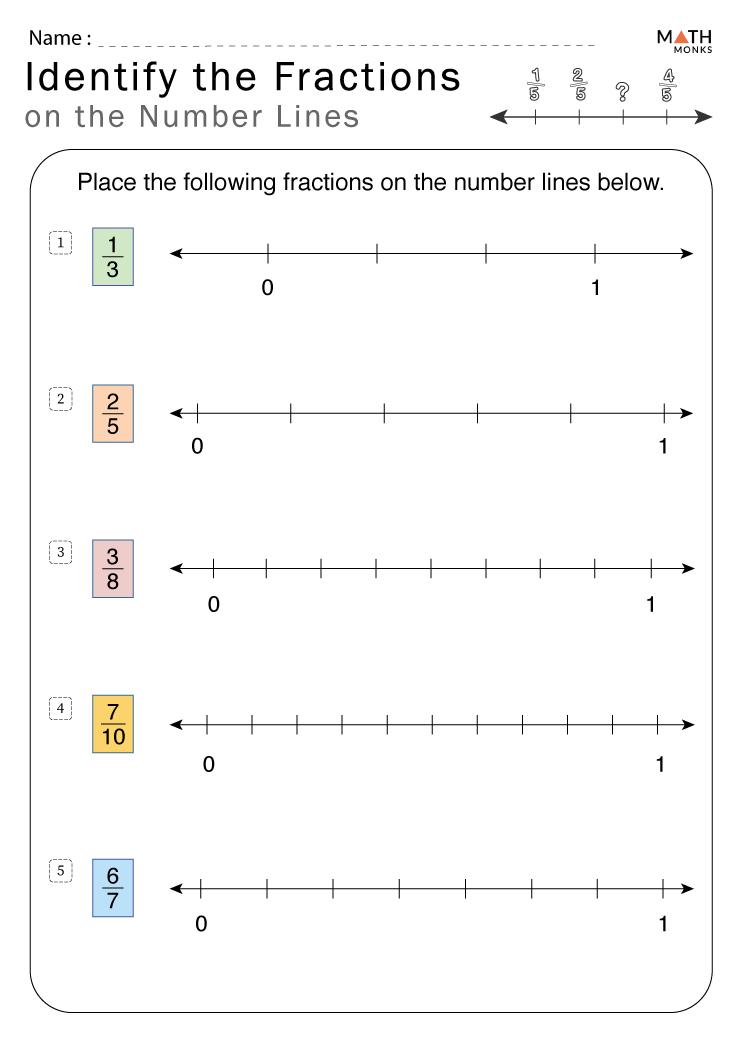
Factor Polynomials Like a Pro: Answer Key and Solutions

Introduction to Factoring Polynomials
Factoring polynomials is a crucial concept in algebra that can be challenging to grasp at first, but with practice and patience, anyone can master it. In this blog post, we’ll explore the world of factoring polynomials, discuss various techniques, and provide examples to help you become a pro at factoring.
What is Factoring Polynomials?
Factoring polynomials involves expressing a polynomial as a product of simpler polynomials, called factors. This process helps us to simplify complex expressions, solve equations, and find the roots of polynomials.
Techniques for Factoring Polynomials
There are several techniques for factoring polynomials, including:
- Greatest Common Factor (GCF)
- Difference of Squares
- Sum and Difference of Cubes
- Factoring by Grouping
- Synthetic Division
Greatest Common Factor (GCF)
The GCF is the largest expression that divides all the terms of a polynomial without leaving a remainder.
Example: Factor the polynomial 6x^2 + 12x + 18
GCF = 6
Factored form: 6(x^2 + 2x + 3)
Difference of Squares
This technique involves factoring a polynomial that can be written in the form a^2 - b^2.
Example: Factor the polynomial x^2 - 4
Factored form: (x - 2)(x + 2)
Sum and Difference of Cubes
This technique involves factoring a polynomial that can be written in the form a^3 + b^3 or a^3 - b^3.
Example: Factor the polynomial x^3 + 8
Factored form: (x + 2)(x^2 - 2x + 4)
Factoring by Grouping
This technique involves grouping the terms of a polynomial to factor it.
Example: Factor the polynomial x^2 + 2x + 1
Factored form: (x + 1)(x + 1)
Synthetic Division
This technique involves using a table to divide a polynomial by a linear factor.
Example: Factor the polynomial x^2 + 2x + 1 using synthetic division

| 1 | 2 | 1 | |
|---|---|---|---|
| 1 | 1 | 3 | 4 |
Factored form: (x + 1)(x + 1)
📝 Note: Synthetic division is a more advanced technique that requires a good understanding of division and polynomials.
Steps to Factor Polynomials
Here are the general steps to factor polynomials:
- Look for the GCF: Factor out the greatest common factor from all the terms.
- Check for special cases: Look for patterns such as difference of squares, sum and difference of cubes, and factoring by grouping.
- Use synthetic division: If the polynomial cannot be factored using the previous techniques, try using synthetic division.
Examples and Solutions
Example 1: Factor the polynomial x^2 + 5x + 6
Solution: x^2 + 5x + 6 = (x + 3)(x + 2)
Example 2: Factor the polynomial x^3 - 8
Solution: x^3 - 8 = (x - 2)(x^2 + 2x + 4)
Example 3: Factor the polynomial x^2 - 7x + 12
Solution: x^2 - 7x + 12 = (x - 3)(x - 4)
Conclusion
Factoring polynomials is an essential skill in algebra that requires patience, practice, and persistence. By mastering various techniques such as GCF, difference of squares, sum and difference of cubes, factoring by grouping, and synthetic division, you can become a pro at factoring polynomials. Remember to always look for the GCF, check for special cases, and use synthetic division when necessary.
What is the difference between factoring and solving equations?
+Factoring involves expressing a polynomial as a product of simpler polynomials, while solving equations involves finding the values of variables that make the equation true.
Can all polynomials be factored?
+No, not all polynomials can be factored. Some polynomials may be prime and cannot be expressed as a product of simpler polynomials.
What is the most important technique for factoring polynomials?
+The GCF is the most important technique for factoring polynomials, as it is used in many other techniques and is often the first step in factoring.
Related Terms:
- Factoring polynomials examples with solutions