Mastering Angle Relationships with Worksheets

Mastering Angle Relationships with Worksheets
Angle relationships are a crucial concept in geometry, and mastering them is essential for solving various problems in mathematics and real-life applications. In this article, we will explore the different types of angle relationships, provide examples, and offer worksheets to help you practice and reinforce your understanding.
Types of Angle Relationships
There are several types of angle relationships, including:
- Complementary angles: Two angles whose sum is 90 degrees.
- Supplementary angles: Two angles whose sum is 180 degrees.
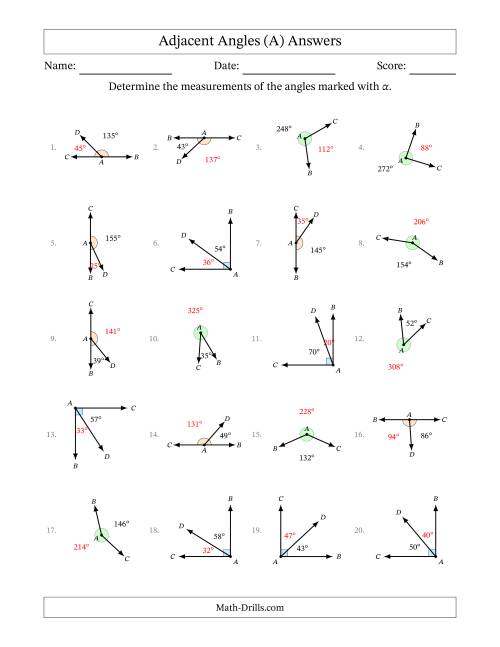
- Adjacent angles: Two angles that share a common side and vertex.
- Vertical angles: Two angles that are opposite each other and share a common vertex.
- Corresponding angles: Two angles that are in the same relative position in two intersecting lines.
- Alternate interior angles: Two angles that are inside the two lines and on opposite sides of the transversal.
- Alternate exterior angles: Two angles that are outside the two lines and on opposite sides of the transversal.
Worksheets for Angle Relationships
To help you master angle relationships, we have provided several worksheets that you can use to practice and reinforce your understanding.
Worksheet 1: Complementary and Supplementary Angles
| Angle 1 | Angle 2 | Sum |
|---|---|---|
| 30 | 60 | 90 |
| 45 | 45 | 90 |
| 20 | 160 | 180 |
| 90 | 90 | 180 |
| 15 | 75 | 90 |
Instructions: Identify whether each pair of angles is complementary or supplementary.
Worksheet 2: Adjacent and Vertical Angles
| Angle 1 | Angle 2 | Relationship |
|---|---|---|
| ∠A | ∠B | Adjacent |
| ∠C | ∠D | Vertical |
| ∠E | ∠F | Adjacent |
| ∠G | ∠H | Vertical |
Instructions: Identify whether each pair of angles is adjacent or vertical.
Worksheet 3: Corresponding and Alternate Angles
| Angle 1 | Angle 2 | Relationship |
|---|---|---|
| ∠A | ∠B | Corresponding |
| ∠C | ∠D | Alternate Interior |
| ∠E | ∠F | Corresponding |
| ∠G | ∠H | Alternate Exterior |
Instructions: Identify whether each pair of angles is corresponding or alternate.
📝 Note: Make sure to check your answers carefully and use a protractor to measure the angles if necessary.
Real-World Applications of Angle Relationships
Angle relationships are not just limited to mathematics; they have numerous real-world applications, including:
- Architecture: Understanding angle relationships is crucial for designing buildings, bridges, and other structures.
- Engineering: Angle relationships are used in the design of machines, mechanisms, and other engineering applications.
- Art and Design: Angle relationships are used in art and design to create balanced and visually appealing compositions.
Conclusion
Mastering angle relationships is essential for problem-solving and critical thinking. By practicing with worksheets and understanding the different types of angle relationships, you can develop a strong foundation in geometry and improve your skills in various real-world applications.
Remember to use a protractor to measure angles accurately and check your answers carefully.
What is the difference between complementary and supplementary angles?
+Complementary angles are two angles whose sum is 90 degrees, while supplementary angles are two angles whose sum is 180 degrees.
How can I identify corresponding angles?
+Corresponding angles are two angles that are in the same relative position in two intersecting lines.
What are some real-world applications of angle relationships?
+Angle relationships are used in architecture, engineering, art, and design to create balanced and visually appealing compositions.