5 Essential Angle Pair Relationship Tips
Unlocking the Secrets of Angle Pair Relationships in Geometry
In the realm of geometry, angle pair relationships are a fundamental concept that helps students understand the intricate connections between angles. These relationships are crucial in solving various geometric problems and theorems. In this article, we will delve into the world of angle pair relationships, exploring five essential tips to help you master this concept.
Tip 1: Understanding the Basics of Angle Pairs
To grasp angle pair relationships, it’s essential to start with the basics. An angle pair is a set of two angles that are related in some way. There are several types of angle pairs, including:
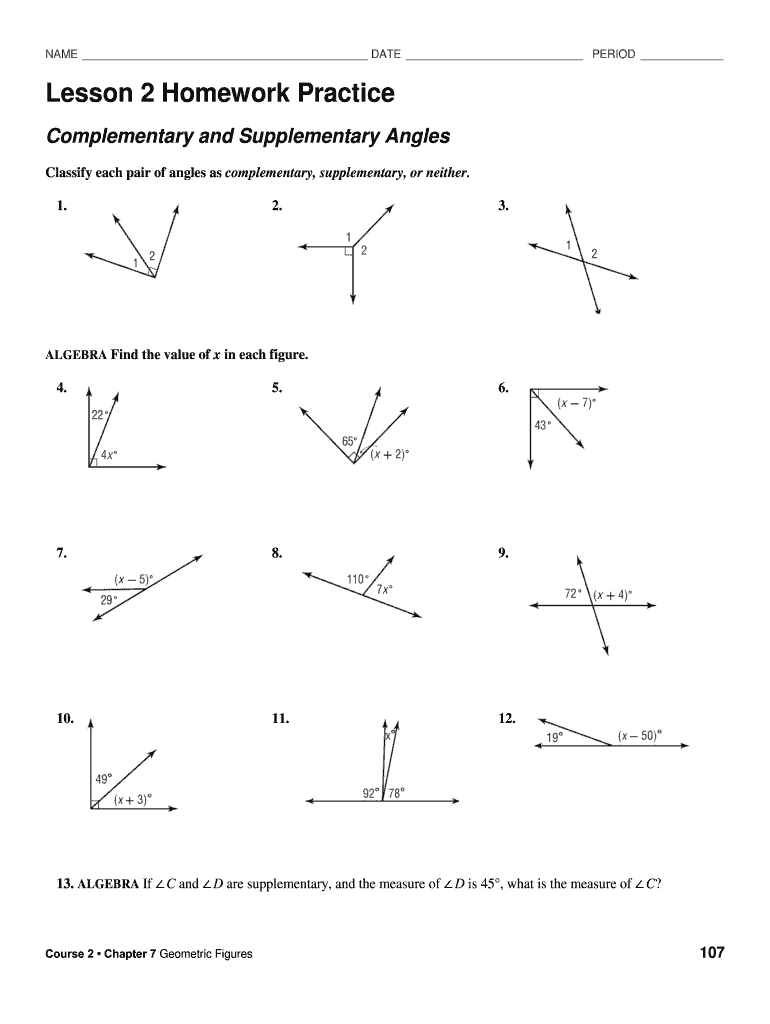
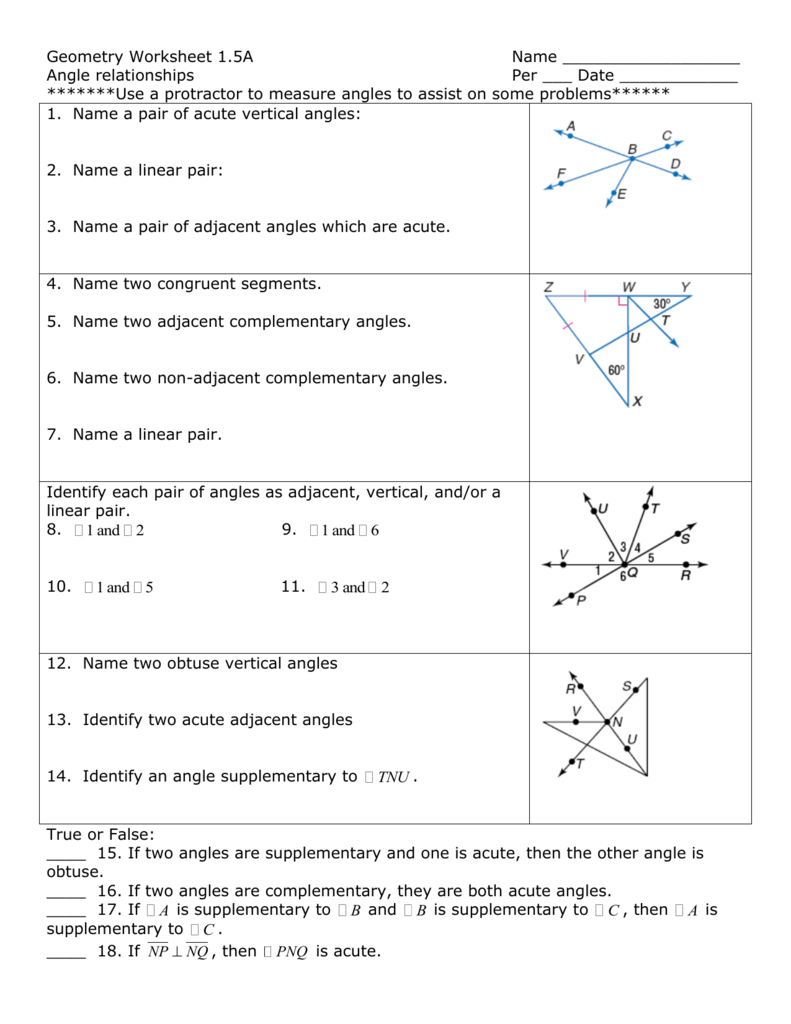
- Linear Pair: Two angles that form a straight line, with their sum equal to 180 degrees.
- Adjacent Pair: Two angles that share a common side and vertex.
- Vertical Pair: Two angles that are opposite each other when two lines intersect.
- Complementary Pair: Two angles whose sum is 90 degrees.
- Supplementary Pair: Two angles whose sum is 180 degrees.
📝 Note: Understanding the definitions of these angle pairs is crucial in identifying and working with angle pair relationships.
Tip 2: Identifying Angle Pairs in Different Geometric Shapes
Angle pairs can be found in various geometric shapes, including triangles, quadrilaterals, and polygons. Here are some key points to remember:
- Triangles: In a triangle, the sum of the interior angles is always 180 degrees. This means that any two angles in a triangle form a supplementary pair.
- Quadrilaterals: In a quadrilateral, the sum of the interior angles is 360 degrees. This means that any two adjacent angles in a quadrilateral form a linear pair.
- Polygons: In a polygon, the sum of the interior angles depends on the number of sides. However, any two adjacent angles in a polygon form a linear pair.
Tip 3: Using Angle Pair Relationships to Solve Problems
Angle pair relationships can be used to solve various geometric problems. Here are some examples:
- Finding Missing Angles: If you know one angle in a linear pair, you can find the other angle by subtracting the known angle from 180 degrees.
- Determining Congruent Angles: If two angles are vertical or corresponding, they are congruent.
- Identifying Similar Triangles: If two triangles have the same angle measures, they are similar.
📝 Note: Angle pair relationships can be used to solve a wide range of geometric problems, from simple angle measurements to complex proofs.
Tip 4: Applying Angle Pair Relationships to Real-World Scenarios
Angle pair relationships are not just limited to geometric shapes; they can be applied to real-world scenarios as well. Here are some examples:
- Architecture: Angle pair relationships are used in building design to ensure that structures are stable and balanced.
- Engineering: Angle pair relationships are used in engineering to design and optimize systems, such as bridges and machines.
- Art and Design: Angle pair relationships are used in art and design to create visually appealing and balanced compositions.
Tip 5: Practicing Angle Pair Relationships with Real-World Examples
To master angle pair relationships, it’s essential to practice with real-world examples. Here are some exercises to try:
- Identify Angle Pairs: Identify angle pairs in different geometric shapes, such as triangles, quadrilaterals, and polygons.
- Solve Angle Problems: Solve problems that involve finding missing angles, determining congruent angles, and identifying similar triangles.
- Apply Angle Pair Relationships: Apply angle pair relationships to real-world scenarios, such as architecture, engineering, and art and design.
| Angle Pair | Definition | Example |
|---|---|---|
| Linear Pair | Two angles that form a straight line, with their sum equal to 180 degrees. | ∠A and ∠B form a linear pair, with ∠A + ∠B = 180° |
| Adjacent Pair | Two angles that share a common side and vertex. | ∠C and ∠D are adjacent angles, with a common side and vertex. |
| Vertical Pair | Two angles that are opposite each other when two lines intersect. | ∠E and ∠F are vertical angles, with ∠E = ∠F. |
| Complementary Pair | Two angles whose sum is 90 degrees. | ∠G and ∠H are complementary angles, with ∠G + ∠H = 90° |
| Supplementary Pair | Two angles whose sum is 180 degrees. | ∠I and ∠J are supplementary angles, with ∠I + ∠J = 180° |
By mastering angle pair relationships, you’ll be able to tackle a wide range of geometric problems with confidence. Remember to practice regularly, applying angle pair relationships to real-world scenarios to reinforce your understanding. With time and practice, you’ll become proficient in using angle pair relationships to solve complex geometric problems.
In summary, angle pair relationships are a fundamental concept in geometry that helps students understand the connections between angles. By understanding the basics of angle pairs, identifying angle pairs in different geometric shapes, using angle pair relationships to solve problems, applying angle pair relationships to real-world scenarios, and practicing with real-world examples, you’ll be well on your way to mastering this essential concept.
What is an angle pair?
+An angle pair is a set of two angles that are related in some way. There are several types of angle pairs, including linear pairs, adjacent pairs, vertical pairs, complementary pairs, and supplementary pairs.
How do I identify angle pairs in different geometric shapes?
+To identify angle pairs in different geometric shapes, look for angles that share a common side and vertex, form a straight line, or are opposite each other when two lines intersect.
How can I use angle pair relationships to solve problems?
+Angle pair relationships can be used to solve a wide range of geometric problems, from finding missing angles to determining congruent angles and identifying similar triangles.
Related Terms:
- Angle pair Relationships Worksheet PDF
- Angle pairs Worksheet grade 7