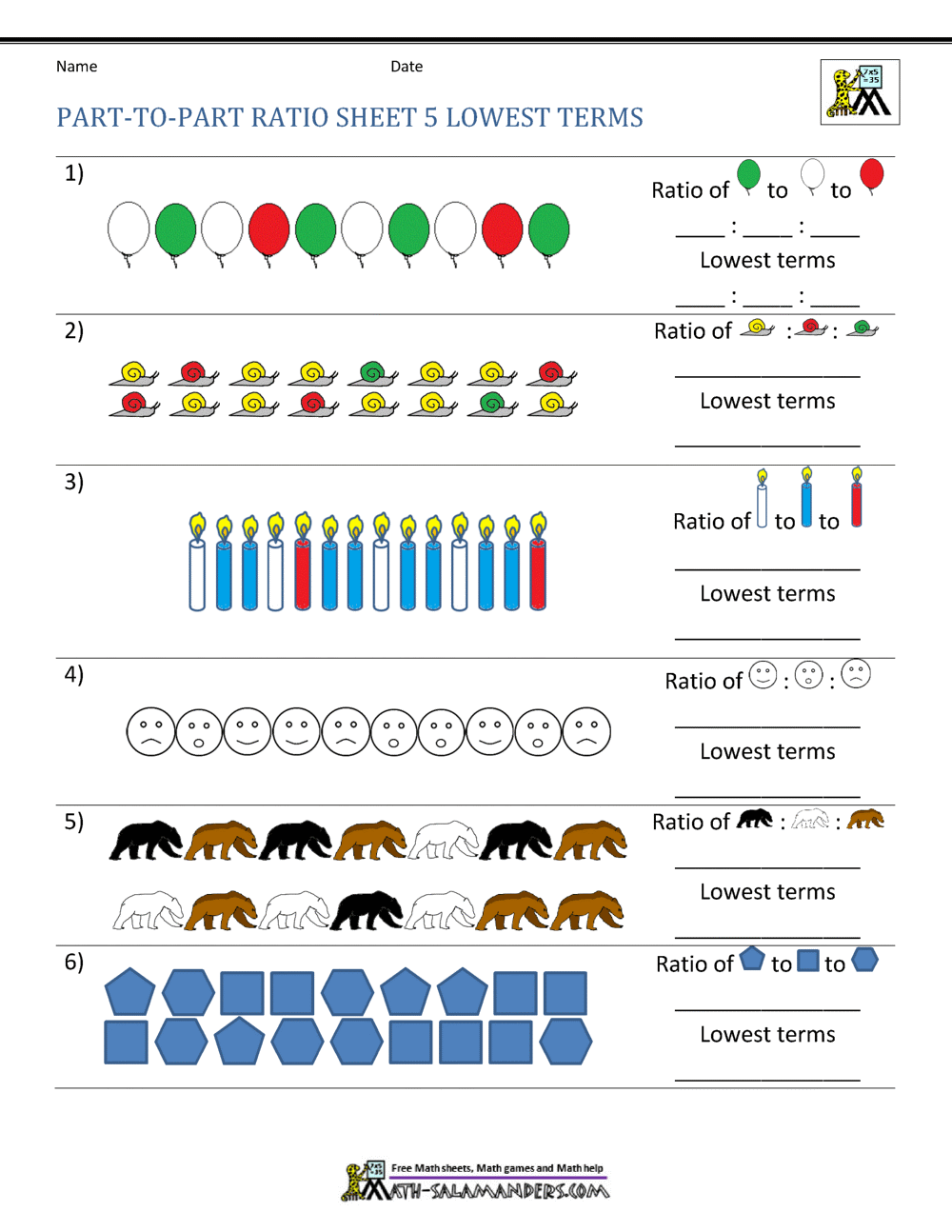
5 Ways to Simplify Algebraic Expressions
Unlocking the Secrets of Algebra: Simplifying Expressions with Ease
Algebraic expressions can be daunting, but with the right strategies, you can simplify them with ease. Whether you’re a student or a professional, mastering the art of simplifying algebraic expressions is crucial for problem-solving and critical thinking. In this article, we’ll explore five ways to simplify algebraic expressions, making it easier for you to tackle complex mathematical problems.
Method 1: Combining Like Terms
Combining like terms is one of the most straightforward methods for simplifying algebraic expressions. This involves adding or subtracting terms that have the same variable and coefficient. For example:
Expression: 2x + 3x + 4
Simplified Expression: 5x + 4
To combine like terms, follow these steps:
- Identify the terms with the same variable and coefficient.
- Add or subtract the coefficients of the like terms.
- Write the simplified expression by combining the like terms.
📝 Note: When combining like terms, make sure to add or subtract the coefficients, not the variables.
Method 2: Factoring Out the Greatest Common Factor (GCF)
Factoring out the GCF is a powerful method for simplifying algebraic expressions. This involves finding the greatest common factor of the terms and factoring it out. For example:
Expression: 12x + 18
Simplified Expression: 6(2x + 3)
To factor out the GCF, follow these steps:
- Find the greatest common factor of the terms.
- Factor out the GCF by dividing each term by the GCF.
- Write the simplified expression by multiplying the GCF by the resulting terms.

| Term | GCF | Resulting Term |
|---|---|---|
| 12x | 6 | 2x |
| 18 | 6 | 3 |
Method 3: Canceling Out Common Factors
Canceling out common factors is another effective method for simplifying algebraic expressions. This involves canceling out common factors between the numerator and denominator of a fraction. For example:
Expression: (6x + 12) / 2
Simplified Expression: 3x + 6
To cancel out common factors, follow these steps:
- Identify the common factors between the numerator and denominator.
- Cancel out the common factors by dividing both the numerator and denominator by the common factor.
- Write the simplified expression by simplifying the resulting fraction.
📝 Note: When canceling out common factors, make sure to divide both the numerator and denominator by the common factor.
Method 4: Using the Distributive Property
The distributive property is a fundamental concept in algebra that can be used to simplify expressions. This involves distributing a single term to multiple terms inside parentheses. For example:
Expression: 2(x + 3)
Simplified Expression: 2x + 6
To use the distributive property, follow these steps:
- Identify the single term outside the parentheses.
- Distribute the single term to each term inside the parentheses.
- Write the simplified expression by combining like terms.
Method 5: Simplifying Exponents
Simplifying exponents is an essential method for simplifying algebraic expressions. This involves using the rules of exponents to simplify expressions with multiple exponents. For example:
Expression: x^2 * x^3
Simplified Expression: x^5
To simplify exponents, follow these steps:
- Identify the rules of exponents (e.g., product rule, power rule).
- Apply the rules of exponents to simplify the expression.
- Write the simplified expression by combining like terms.
In conclusion, simplifying algebraic expressions is a crucial skill for problem-solving and critical thinking. By mastering the five methods outlined in this article, you’ll be able to tackle complex mathematical problems with ease. Remember to practice regularly and apply these methods to different types of expressions to become a pro at simplifying algebraic expressions.
What is the difference between combining like terms and factoring out the GCF?
+Combining like terms involves adding or subtracting terms with the same variable and coefficient, while factoring out the GCF involves finding the greatest common factor of the terms and factoring it out.
Can I use the distributive property to simplify expressions with multiple variables?
+How do I know which method to use to simplify an algebraic expression?
+It depends on the type of expression and the context. Try to identify the simplest method first, and then apply more complex methods if necessary.