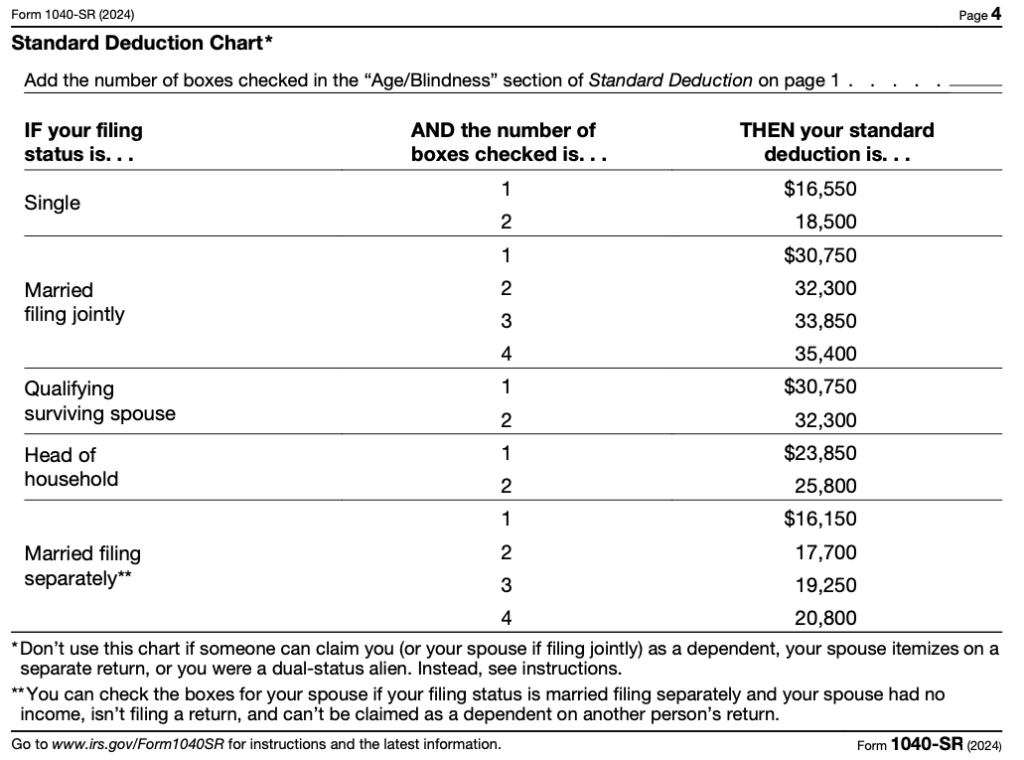
Fractions Made Easy: Adding and Subtracting Unlike Denominators

Understanding Fractions with Unlike Denominators

When working with fractions, one of the most challenging concepts to grasp is adding and subtracting unlike denominators. Unlike denominators refer to fractions that have different denominators, making it difficult to perform arithmetic operations. However, with the right approach and techniques, you can easily add and subtract fractions with unlike denominators.

What are Unlike Denominators?

Unlike denominators occur when two or more fractions have different denominators. For example:

• ¹⁄₄ and ¹⁄₆
• ²⁄₃ and ³⁄₅
• ³⁄₈ and ²⁄₇

In each of these examples, the fractions have different denominators, making it challenging to add or subtract them directly.

How to Add Fractions with Unlike Denominators

To add fractions with unlike denominators, you need to follow these steps:

1. Find the Least Common Multiple (LCM): The first step is to find the least common multiple (LCM) of the two denominators. The LCM is the smallest number that both denominators can divide into evenly.
2. Convert both fractions to have the LCM as the denominator: Once you have found the LCM, you need to convert both fractions to have the LCM as the denominator. You can do this by multiplying the numerator and denominator of each fraction by the necessary multiplier.
3. Add the fractions: Once both fractions have the same denominator, you can add them by adding the numerators and keeping the same denominator.

Let’s use the example of adding ¹⁄₄ and ¹⁄₆:

1. Find the LCM of 4 and 6, which is 12.
2. Convert both fractions to have a denominator of 12:
   • ¹⁄₄ = ³⁄₁₂
   • ¹⁄₆ = ²⁄₁₂
3. Add the fractions: ³⁄₁₂ + ²⁄₁₂ = ⁵⁄₁₂

How to Subtract Fractions with Unlike Denominators

Subtracting fractions with unlike denominators follows the same steps as adding fractions:

1. Find the Least Common Multiple (LCM): Find the LCM of the two denominators.
2. Convert both fractions to have the LCM as the denominator: Convert both fractions to have the LCM as the denominator.
3. Subtract the fractions: Subtract the numerators and keep the same denominator.

Let’s use the example of subtracting ²⁄₃ and ³⁄₅:

1. Find the LCM of 3 and 5, which is 15.
2. Convert both fractions to have a denominator of 15:
   • ²⁄₃ = ¹⁰⁄₁₅
   • ³⁄₅ = ⁹⁄₁₅
3. Subtract the fractions: ¹⁰⁄₁₅ - ⁹⁄₁₅ = ¹⁄₁₅

Important Notes

📝 Note: When adding or subtracting fractions with unlike denominators, make sure to find the LCM of the two denominators. This will ensure that you are working with equivalent fractions.

📝 Note: When converting fractions to have the LCM as the denominator, make sure to multiply both the numerator and denominator by the necessary multiplier.

Conclusion

Adding and subtracting fractions with unlike denominators can be challenging, but with the right approach and techniques, you can easily perform these operations. Remember to find the LCM of the two denominators and convert both fractions to have the LCM as the denominator. By following these steps, you can add and subtract fractions with unlike denominators with confidence.