5 Easy Steps to Add Fractions With Unlike Denominators

Adding Fractions with Unlike Denominators: A Simple Guide
Adding fractions with unlike denominators can be a bit tricky, but with the right approach, it can be made easy. In this guide, we will walk you through the process of adding fractions with unlike denominators in 5 easy steps.
What are Unlike Denominators?
Before we dive into the steps, let’s first understand what unlike denominators are. Unlike denominators refer to fractions that have different denominators. For example, 1⁄4 and 1⁄6 are fractions with unlike denominators because their denominators (4 and 6) are not the same.
Step 1: Identify the Denominators
To add fractions with unlike denominators, the first step is to identify the denominators of the fractions you want to add. In our example, the denominators are 4 and 6.
📝 Note: Make sure to write down the denominators of the fractions you want to add.
Step 2: Find the Least Common Multiple (LCM)
The next step is to find the least common multiple (LCM) of the denominators. The LCM is the smallest number that both denominators can divide into evenly. To find the LCM, you can list the multiples of each denominator and find the smallest number that appears in both lists.
For example, the multiples of 4 are: 4, 8, 12, 16, 20, 24,… The multiples of 6 are: 6, 12, 18, 24, 30,…
As you can see, the smallest number that appears in both lists is 12. Therefore, the LCM of 4 and 6 is 12.
Step 3: Convert the Fractions to Equivalent Fractions with the LCM
Now that we have the LCM, we need to convert each fraction to an equivalent fraction with the LCM as the denominator. To do this, we need to multiply the numerator and denominator of each fraction by the same number.
For example, to convert 1⁄4 to an equivalent fraction with a denominator of 12, we need to multiply the numerator and denominator by 3.
1⁄4 = (1 x 3) / (4 x 3) = 3⁄12
Similarly, to convert 1⁄6 to an equivalent fraction with a denominator of 12, we need to multiply the numerator and denominator by 2.
1⁄6 = (1 x 2) / (6 x 2) = 2⁄12
Step 4: Add the Fractions
Now that we have equivalent fractions with the same denominator, we can add them.
3⁄12 + 2⁄12 = 5⁄12
Step 5: Simplify the Answer (Optional)
Finally, we can simplify the answer by dividing the numerator and denominator by the greatest common divisor (GCD).
In this case, the GCD of 5 and 12 is 1, so we cannot simplify the answer further.
And that’s it! With these 5 easy steps, you can add fractions with unlike denominators.
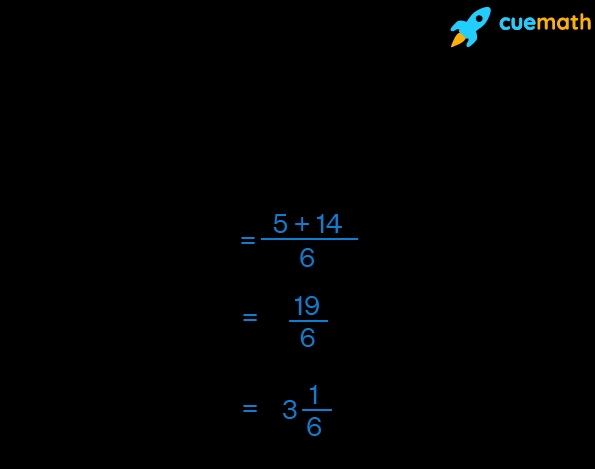
| Step | Description |
|---|---|
| 1 | Identify the denominators |
| 2 | Find the least common multiple (LCM) |
| 3 | Convert the fractions to equivalent fractions with the LCM |
| 4 | Add the fractions |
| 5 | Simplify the answer (optional) |
In summary, adding fractions with unlike denominators involves identifying the denominators, finding the LCM, converting the fractions to equivalent fractions with the LCM, adding the fractions, and simplifying the answer (if necessary). By following these steps, you can easily add fractions with unlike denominators.
What is the least common multiple (LCM)?
+The least common multiple (LCM) is the smallest number that two or more numbers can divide into evenly.
How do I find the LCM of two numbers?
+To find the LCM of two numbers, list the multiples of each number and find the smallest number that appears in both lists.
Can I simplify the answer after adding fractions with unlike denominators?
+Yes, you can simplify the answer by dividing the numerator and denominator by the greatest common divisor (GCD).



