Add Fractions With Different Denominators Made Easy
Add Fractions With Different Denominators Made Easy
Are you struggling to add fractions with different denominators? Do you find it challenging to simplify your answers? Look no further! In this article, we will walk you through a step-by-step guide on how to add fractions with different denominators. By the end of this tutorial, you will be able to confidently add fractions with ease.
Understanding the Concept of Denominators
Before we dive into adding fractions, let’s first understand the concept of denominators. The denominator is the number that appears at the bottom of a fraction. It tells us how many equal parts something is divided into. For example, in the fraction 3⁄4, the denominator is 4. This means that the whole is divided into 4 equal parts, and we have 3 of those parts.
Why Adding Fractions with Different Denominators is Challenging
Adding fractions with different denominators can be challenging because we need to find a common ground to compare them. Think of it like trying to add apples and oranges - they are different units, and we need to find a way to make them compatible. In fractions, this common ground is called the least common multiple (LCM).
How to Find the Least Common Multiple (LCM)
To find the LCM of two numbers, we need to list their multiples and find the smallest number that appears in both lists. Here’s an example:
- Multiples of 4: 4, 8, 12, 16, 20
- Multiples of 6: 6, 12, 18, 24, 30
As you can see, the smallest number that appears in both lists is 12. Therefore, the LCM of 4 and 6 is 12.
Step-by-Step Guide to Adding Fractions with Different Denominators
Now that we understand the concept of denominators and LCM, let’s move on to the step-by-step guide:
Step 1: List the Multiples of Each Denominator
Write down the multiples of each denominator to find the LCM.
Step 2: Find the LCM
Identify the smallest number that appears in both lists of multiples.
Step 3: Convert Each Fraction to Have the LCM as the Denominator
Multiply the numerator and denominator of each fraction by the necessary number to get the LCM as the denominator.
Step 4: Add the Fractions
Now that both fractions have the same denominator, we can add them by adding the numerators.
Step 5: Simplify the Answer
If possible, simplify the fraction by dividing both the numerator and denominator by the greatest common divisor (GCD).
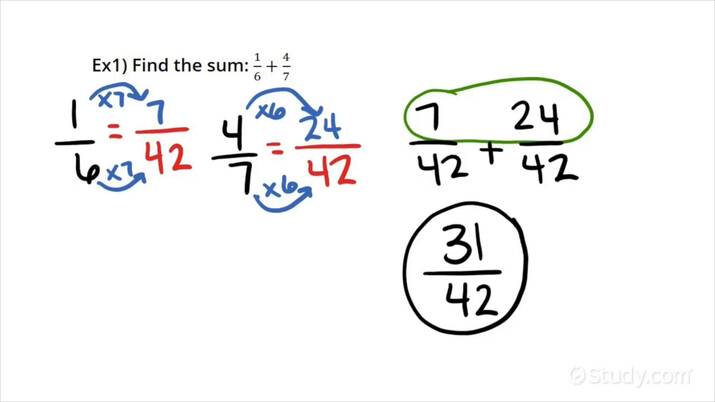
Example 1: Adding Fractions with Different Denominators
Let’s say we want to add the fractions 1⁄4 and 1⁄6.
Step 1: List the Multiples of Each Denominator
- Multiples of 4: 4, 8, 12, 16, 20
- Multiples of 6: 6, 12, 18, 24, 30
Step 2: Find the LCM
The LCM of 4 and 6 is 12.
Step 3: Convert Each Fraction to Have the LCM as the Denominator
- 1⁄4 = (1 x 3)/(4 x 3) = 3⁄12
- 1⁄6 = (1 x 2)/(6 x 2) = 2⁄12
Step 4: Add the Fractions
3⁄12 + 2⁄12 = 5⁄12
Step 5: Simplify the Answer
The fraction 5⁄12 is already in its simplest form.
🤔 Note: When adding fractions with different denominators, it's essential to find the LCM to ensure that both fractions have the same denominator.
Common Mistakes to Avoid When Adding Fractions
Here are some common mistakes to avoid when adding fractions:
- Not finding the LCM: Make sure to find the LCM of both denominators before adding the fractions.
- Not converting each fraction to have the LCM as the denominator: Ensure that both fractions have the same denominator before adding them.
- Not simplifying the answer: Always simplify the fraction after adding it to ensure that it’s in its simplest form.
Practice Exercises
Now that you’ve learned how to add fractions with different denominators, it’s time to practice! Try solving these exercises:
- 1⁄2 + 1⁄3 =
- 2⁄5 + 3⁄7 =
- 3⁄8 + 2⁄9 =
Check your answers to see if you’re correct!
By following these steps and practicing regularly, you’ll become a pro at adding fractions with different denominators in no time!
Bonus Tip: Using a Table to Find the LCM
Here’s a bonus tip to help you find the LCM quickly:

| Multiples of 4 | Multiples of 6 |
|---|---|
| 4 | 6 |
| 8 | 12 |
| 12 | 18 |
| 16 | 24 |
| 20 | 30 |
By using a table to list the multiples of each denominator, you can quickly identify the LCM.
What is the least common multiple (LCM) of two numbers?
+The LCM of two numbers is the smallest number that appears in both lists of multiples.
Why is it essential to find the LCM when adding fractions with different denominators?
+Finding the LCM ensures that both fractions have the same denominator, making it possible to add them.
How can I simplify a fraction after adding it?
+To simplify a fraction, divide both the numerator and denominator by the greatest common divisor (GCD).
In conclusion, adding fractions with different denominators requires finding the LCM, converting each fraction to have the LCM as the denominator, adding the fractions, and simplifying the answer. By following these steps and practicing regularly, you’ll become proficient in adding fractions with ease.