Solving Absolute Value Equations and Inequalities Made Easy

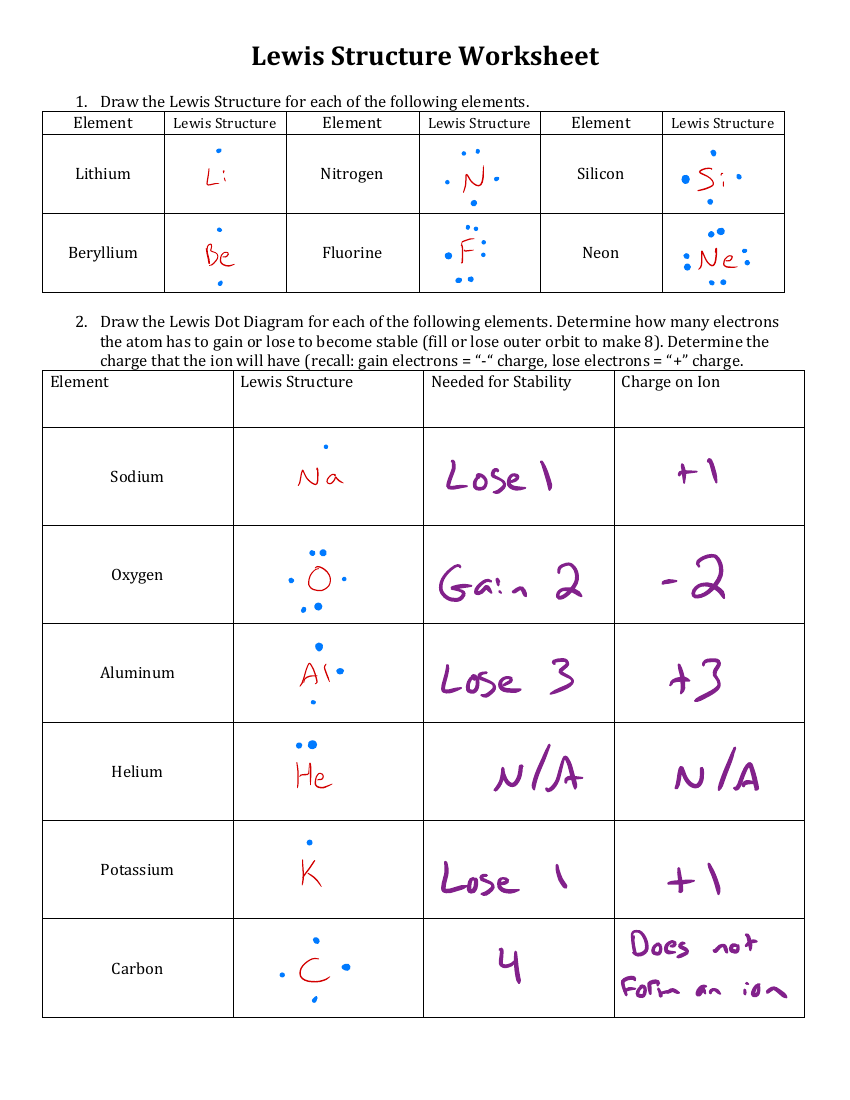
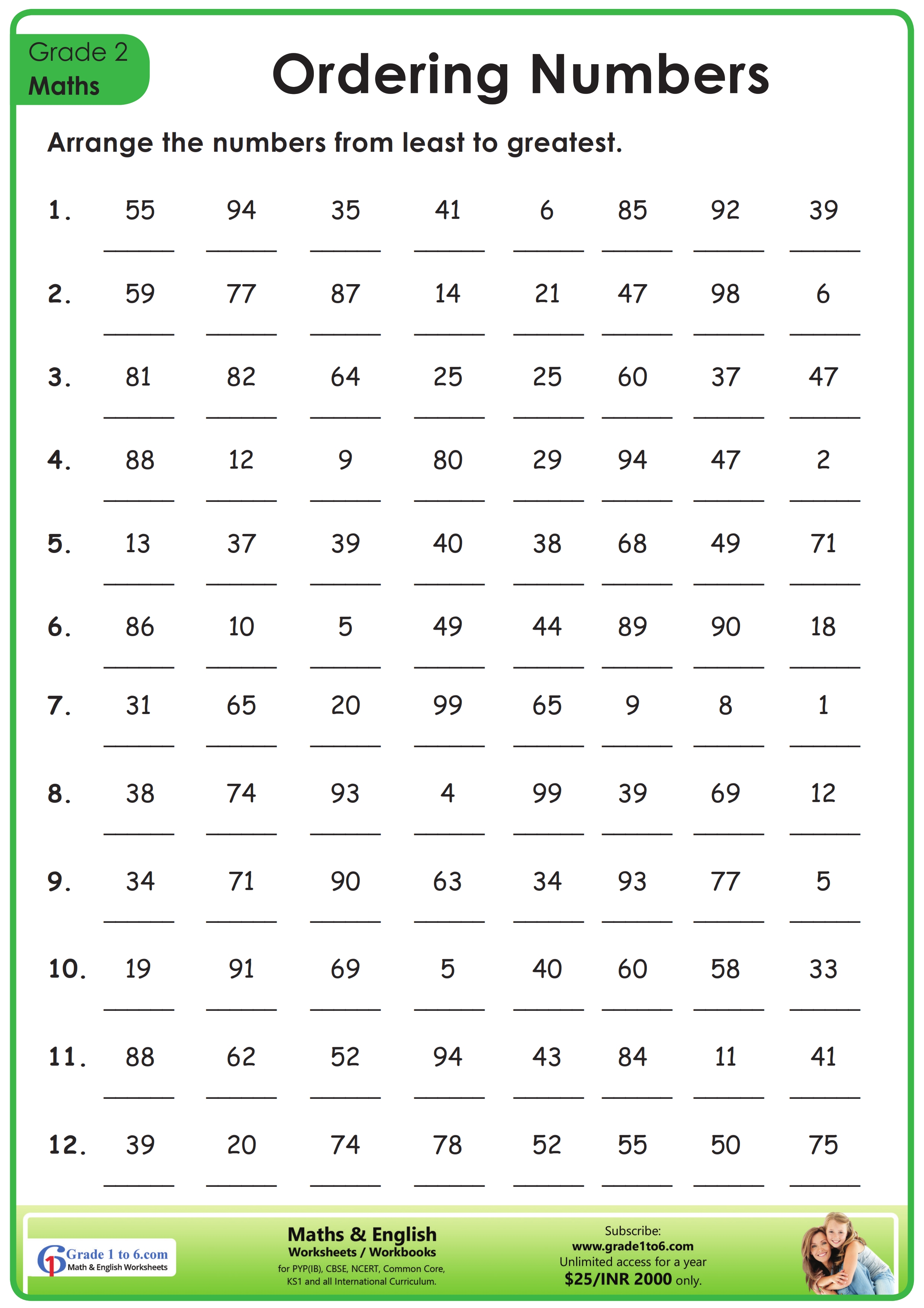
Solving Absolute Value Equations and Inequalities Made Easy
Are you struggling to solve absolute value equations and inequalities? Do you find yourself getting confused with the different rules and formulas? Don’t worry, you’re not alone! Absolute value equations and inequalities can be tricky, but with the right approach, you can master them in no time.
What is Absolute Value?
Before we dive into solving equations and inequalities, let’s quickly review what absolute value is. The absolute value of a number is its distance from zero on the number line. It’s denoted by two vertical lines | | and is always non-negative. For example, the absolute value of 5 is |5| = 5, and the absolute value of -3 is |-3| = 3.
Solving Absolute Value Equations
Now that we’ve got the basics covered, let’s move on to solving absolute value equations. An absolute value equation is an equation that contains an absolute value expression. Here are the general steps to solve an absolute value equation:
- Isolate the absolute value expression: Get the absolute value expression by itself on one side of the equation.
- Set up two equations: Write two separate equations based on the definition of absolute value:
- One equation where the expression inside the absolute value bars is positive.
- One equation where the expression inside the absolute value bars is negative.
- Solve each equation: Solve each of the two equations separately.
👉 Note: Make sure to check your solutions in the original equation to ensure they are valid.
Let’s try an example:
|2x - 3| = 5
To solve this equation, we’ll follow the steps:
- Isolate the absolute value expression: |2x - 3| = 5
- Set up two equations:
- 2x - 3 = 5
- 2x - 3 = -5
- Solve each equation:
- 2x - 3 = 5 –> 2x = 8 –> x = 4
- 2x - 3 = -5 –> 2x = -2 –> x = -1
So, the solutions are x = 4 and x = -1.
Solving Absolute Value Inequalities
Solving absolute value inequalities is a bit trickier than solving equations, but don’t worry, we’ve got this! An absolute value inequality is an inequality that contains an absolute value expression. Here are the general steps to solve an absolute value inequality:
- Isolate the absolute value expression: Get the absolute value expression by itself on one side of the inequality.
- Determine the direction of the inequality: Determine whether the inequality is “less than” or “greater than”.
- Set up two inequalities: Write two separate inequalities based on the definition of absolute value:
- One inequality where the expression inside the absolute value bars is positive.
- One inequality where the expression inside the absolute value bars is negative.
- Solve each inequality: Solve each of the two inequalities separately.
👉 Note: Make sure to check your solutions in the original inequality to ensure they are valid.
Let’s try an example:
|3x + 2| < 7
To solve this inequality, we’ll follow the steps:
- Isolate the absolute value expression: |3x + 2| < 7
- Determine the direction of the inequality: The inequality is “less than”.
- Set up two inequalities:
- 3x + 2 < 7
- 3x + 2 > -7
- Solve each inequality:
- 3x + 2 < 7 –> 3x < 5 –> x < 5⁄3
- 3x + 2 > -7 –> 3x > -9 –> x > -3
So, the solutions are x < 5⁄3 and x > -3.
Tips and Tricks
Here are some tips and tricks to help you master solving absolute value equations and inequalities:
- Pay attention to the direction of the inequality: Make sure to determine whether the inequality is “less than” or “greater than” to set up the correct inequalities.
- Check your solutions: Always check your solutions in the original equation or inequality to ensure they are valid.
- Use the definition of absolute value: Use the definition of absolute value to set up the correct equations or inequalities.
- Practice, practice, practice!: The more you practice, the more comfortable you’ll become with solving absolute value equations and inequalities.
Here is a table summarizing the steps to solve absolute value equations and inequalities:

| Equation/Inequality | Steps to Solve |
|---|---|
| Absolute Value Equation |
1. Isolate the absolute value expression 2. Set up two equations 3. Solve each equation |
| Absolute Value Inequality |
1. Isolate the absolute value expression 2. Determine the direction of the inequality 3. Set up two inequalities 4. Solve each inequality |
In conclusion, solving absolute value equations and inequalities requires attention to detail and a solid understanding of the definition of absolute value. By following the steps outlined in this post and practicing regularly, you’ll become proficient in solving these types of equations and inequalities in no time.
What is the difference between an absolute value equation and an absolute value inequality?
+An absolute value equation is an equation that contains an absolute value expression, whereas an absolute value inequality is an inequality that contains an absolute value expression.
How do I determine the direction of an absolute value inequality?
+To determine the direction of an absolute value inequality, look at the inequality symbol. If it’s “less than”, the inequality is in the direction of the negative values. If it’s “greater than”, the inequality is in the direction of the positive values.
Why do I need to check my solutions in the original equation or inequality?
+Checking your solutions in the original equation or inequality ensures that they are valid and not extraneous. This is especially important when solving absolute value equations and inequalities, as the solutions can be sensitive to the direction of the inequality.
Related Terms:
- Absolute value Inequalities pdf
- Double absolute value Inequalities pdf
- Absolute Value Equations Worksheet pdf