5 Ways to Write Equations of Lines
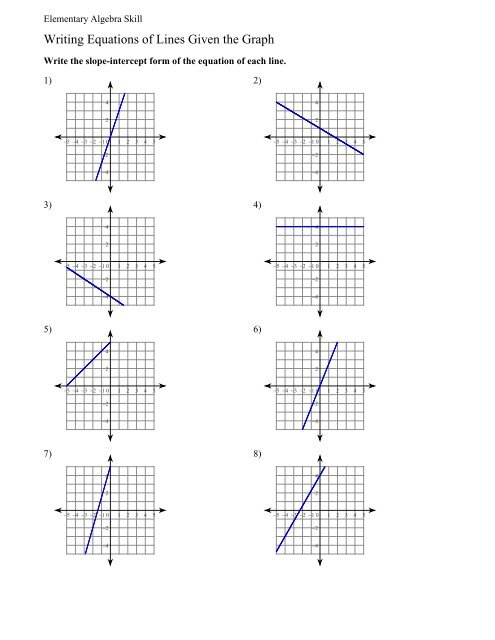
Understanding the Basics of Writing Equations of Lines
When it comes to writing equations of lines, there are several methods to achieve the same goal. In this article, we will explore five different ways to write equations of lines, each with its unique approach and application. Whether you’re a student or a professional, mastering these methods will help you to effectively communicate mathematical ideas and solve problems.
Method 1: Slope-Intercept Form (y = mx + b)
The slope-intercept form is one of the most common methods of writing equations of lines. This method involves expressing the equation in the form y = mx + b, where m represents the slope of the line and b represents the y-intercept.
📝 Note: The slope-intercept form is useful for graphing lines, as it provides a clear visual representation of the line's slope and y-intercept.
For example, if we have a line with a slope of 2 and a y-intercept of 3, the equation of the line in slope-intercept form would be:
y = 2x + 3
Method 2: Standard Form (Ax + By = C)
The standard form of writing equations of lines is Ax + By = C, where A, B, and C are constants. This method is useful for finding the equation of a line when given the coordinates of two points on the line.
📝 Note: The standard form is often used in algebra and geometry, as it provides a concise and standardized way of expressing linear equations.
For example, if we have two points on a line, (2, 3) and (4, 5), we can use the standard form to find the equation of the line:
2x + 3y = 12
Method 3: Point-Slope Form (y - y1 = m(x - x1))
The point-slope form is a useful method for finding the equation of a line when given the coordinates of a point on the line and the slope. This method involves expressing the equation in the form y - y1 = m(x - x1), where (x1, y1) is a point on the line and m is the slope.
📝 Note: The point-slope form is often used in calculus and analytical geometry, as it provides a flexible and concise way of expressing linear equations.
For example, if we have a point (2, 3) and a slope of 2, we can use the point-slope form to find the equation of the line:
y - 3 = 2(x - 2)
Method 4: Parametric Form (x = x1 + t, y = y1 + mt)
The parametric form is a method of expressing the equation of a line in terms of a parameter, often represented by the variable t. This method involves expressing the equation in the form x = x1 + t, y = y1 + mt, where (x1, y1) is a point on the line and m is the slope.
📝 Note: The parametric form is often used in physics and engineering, as it provides a convenient way of expressing the position and velocity of an object in terms of time.
For example, if we have a point (2, 3) and a slope of 2, we can use the parametric form to find the equation of the line:
x = 2 + t, y = 3 + 2t
Method 5: Intercept Form (x/a + y/b = 1)
The intercept form is a method of expressing the equation of a line in terms of the x-intercept and y-intercept. This method involves expressing the equation in the form x/a + y/b = 1, where a is the x-intercept and b is the y-intercept.
📝 Note: The intercept form is often used in economics and finance, as it provides a convenient way of expressing the intersection of supply and demand curves.
For example, if we have an x-intercept of 3 and a y-intercept of 4, we can use the intercept form to find the equation of the line:
x/3 + y/4 = 1
In conclusion, there are several ways to write equations of lines, each with its unique advantages and applications. By mastering these methods, you’ll be able to effectively communicate mathematical ideas and solve problems in a variety of fields.
What is the difference between the slope-intercept form and the standard form of writing equations of lines?
+
The slope-intercept form (y = mx + b) is useful for graphing lines and provides a clear visual representation of the line’s slope and y-intercept. The standard form (Ax + By = C) is often used in algebra and geometry, as it provides a concise and standardized way of expressing linear equations.
When would I use the point-slope form of writing equations of lines?
+
The point-slope form (y - y1 = m(x - x1)) is often used when given the coordinates of a point on the line and the slope. It is a flexible and concise way of expressing linear equations, making it useful in calculus and analytical geometry.
What is the advantage of using the parametric form of writing equations of lines?
+
The parametric form (x = x1 + t, y = y1 + mt) provides a convenient way of expressing the position and velocity of an object in terms of time, making it useful in physics and engineering.