Volume of Rectangular Prisms Worksheets Made Easy
Understanding the Concept of Volume of Rectangular Prisms
When it comes to calculating the volume of rectangular prisms, many students find it a bit challenging. However, with a clear understanding of the concept and a few simple formulas, anyone can master this topic. In this article, we will delve into the world of rectangular prisms, explore their properties, and provide a step-by-step guide on how to calculate their volume.
What is a Rectangular Prism?
A rectangular prism is a three-dimensional solid object that has six rectangular faces. It has three dimensions: length, width, and height. Rectangular prisms are commonly found in everyday life, and understanding their properties is essential in various fields such as architecture, engineering, and mathematics.
Properties of Rectangular Prisms
Here are some key properties of rectangular prisms:
- Six rectangular faces: A rectangular prism has six faces, each of which is a rectangle.
- Three dimensions: A rectangular prism has three dimensions: length, width, and height.
- Right angles: All the angles in a rectangular prism are right angles (90 degrees).
How to Calculate the Volume of a Rectangular Prism
The volume of a rectangular prism is the amount of space inside the prism. To calculate the volume, you need to multiply the length, width, and height of the prism.
Volume Formula:
Volume = Length × Width × Height
Example:
Find the volume of a rectangular prism with a length of 6 cm, a width of 4 cm, and a height of 2 cm.
Volume = 6 cm × 4 cm × 2 cm = 48 cubic centimeters (cm³)
📝 Note: Make sure to use the same units for all three dimensions when calculating the volume.
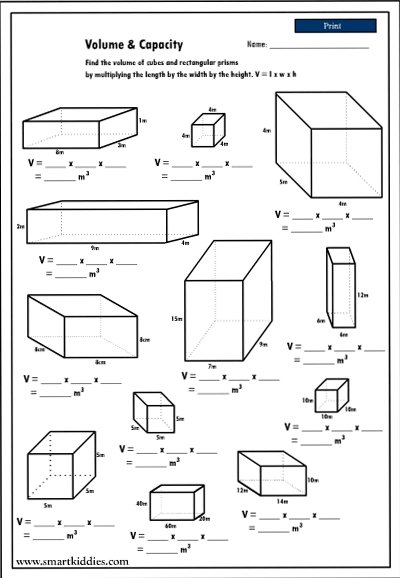
Volume of Rectangular Prisms Worksheets
To help you practice calculating the volume of rectangular prisms, we have provided a few worksheets below. These worksheets cover various scenarios, including different units and decimal calculations.
Worksheet 1: Volume of Rectangular Prisms (cm³)

| Length (cm) | Width (cm) | Height (cm) | Volume (cm³) |
|---|---|---|---|
| 5 | 3 | 2 | ? |
| 8 | 4 | 6 | ? |
| 9 | 6 | 3 | ? |
Worksheet 2: Volume of Rectangular Prisms (m³)
| Length (m) | Width (m) | Height (m) | Volume (m³) |
|---|---|---|---|
| 2 | 1.5 | 0.8 | ? |
| 4 | 2.5 | 1.2 | ? |
| 6 | 3.5 | 2.5 | ? |
Worksheet 3: Volume of Rectangular Prisms (Decimal Calculations)
| Length (cm) | Width (cm) | Height (cm) | Volume (cm³) |
|---|---|---|---|
| 4.5 | 2.8 | 1.9 | ? |
| 7.2 | 3.6 | 2.1 | ? |
| 9.8 | 5.4 | 3.2 | ? |
Tips and Tricks
Here are some tips and tricks to help you master the concept of volume of rectangular prisms:
- Use the formula: Make sure to use the correct formula (Volume = Length × Width × Height) when calculating the volume.
- Check your units: Ensure that you are using the same units for all three dimensions.
- Practice, practice, practice: The more you practice, the more comfortable you will become with calculating the volume of rectangular prisms.
Volume is an essential concept in mathematics, and mastering it will help you solve various problems in geometry, engineering, and architecture. By following the tips and tricks outlined above and practicing with the provided worksheets, you will become proficient in calculating the volume of rectangular prisms.
The concept of volume is a fundamental aspect of mathematics, and understanding it is crucial for solving various problems in geometry, engineering, and architecture. With practice and patience, you can master the art of calculating the volume of rectangular prisms.
What is the formula for calculating the volume of a rectangular prism?
+The formula for calculating the volume of a rectangular prism is: Volume = Length × Width × Height.
What are the properties of a rectangular prism?
+A rectangular prism has six rectangular faces, three dimensions (length, width, and height), and all the angles are right angles (90 degrees).
How do I check if I’m using the correct units when calculating the volume?
+Make sure to use the same units for all three dimensions (length, width, and height) when calculating the volume.