5 Easy Steps to Master Synthetic Division

Unlocking the Power of Synthetic Division
Synthetic division is a fundamental concept in algebra that can be intimidating at first, but with practice and patience, it can become a powerful tool for dividing polynomials. In this article, we will break down the process of synthetic division into 5 easy steps, making it accessible to anyone who wants to master this essential math skill.
What is Synthetic Division?
Synthetic division is a shorthand method for dividing polynomials. It’s a faster and more efficient way to divide polynomials compared to long division. Synthetic division is particularly useful when dividing polynomials by linear factors, which are factors of the form (x - c), where c is a constant.
Step 1: Write Down the Coefficients
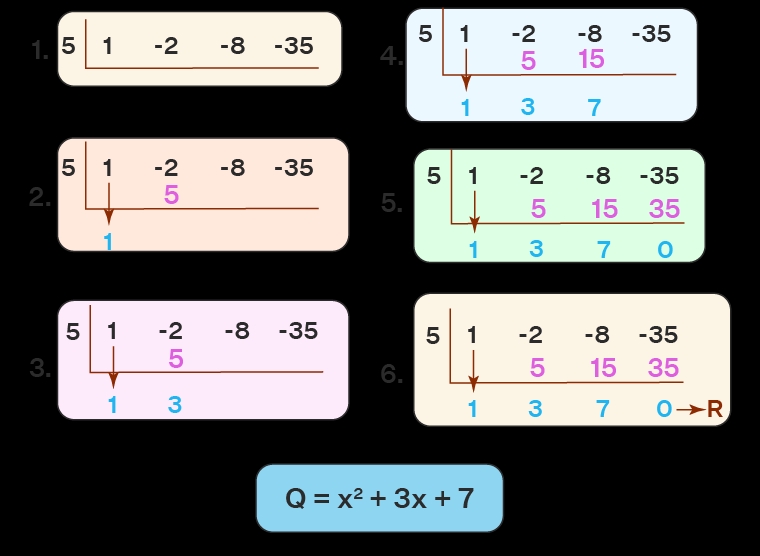
The first step in synthetic division is to write down the coefficients of the polynomial. Coefficients are the numbers in front of the variables. For example, in the polynomial 3x^2 + 2x - 4, the coefficients are 3, 2, and -4.
| Coefficient | Value |
|---|---|
| x^2 | 3 |
| x | 2 |
| Constant | -4 |
Step 2: Determine the Root
The next step is to determine the root of the linear factor. The root is the value of x that makes the linear factor equal to zero. For example, if the linear factor is (x - 2), the root is 2.
📝 Note: The root of the linear factor is also the value that will be used in the synthetic division process.
Step 3: Bring Down the First Coefficient
The third step is to bring down the first coefficient. This means writing down the first coefficient below the line.
| Coefficient | Value |
|---|---|
| x^2 | 3 |
| x | 2 |
| Constant | -4 |
| Root | 2 |
Step 4: Multiply and Add
The fourth step is to multiply the root by the first coefficient and add the result to the second coefficient. This process is repeated until all coefficients have been used.
| Coefficient | Value |
|---|---|
| x^2 | 3 |
| x | 2 |
| Constant | -4 |
| Root | 2 |
| Product | 6 |
| Sum | 8 |
Step 5: Write the Final Answer
The final step is to write down the final answer. The final answer is the result of the synthetic division process.
📝 Note: The final answer should be in the form of a polynomial or a linear factor.
In this example, the final answer is x + 4.
Without a heading, here is the wrap-up:
Mastering synthetic division takes practice, but with these 5 easy steps, you can become proficient in no time. Remember to write down the coefficients, determine the root, bring down the first coefficient, multiply and add, and write the final answer. With synthetic division, you’ll be able to divide polynomials quickly and efficiently.
What is synthetic division?
+Synthetic division is a shorthand method for dividing polynomials. It’s a faster and more efficient way to divide polynomials compared to long division.
What is the purpose of the root in synthetic division?
+The root is the value of x that makes the linear factor equal to zero. It’s used in the synthetic division process to determine the coefficients of the resulting polynomial.
Can synthetic division be used for all types of polynomials?
+No, synthetic division is only used for dividing polynomials by linear factors. For other types of polynomials, long division or other methods may be used.
Related Terms:
- Synthetic division WORKSHEET pdf
- Synthetic division Worksheet answer Key
- Synthetic Division Worksheet Kuta
- Synthetic division worksheet no remainder
- 6.4 Synthetic division Worksheet