Parallel Lines and Transversals Worksheet Explained
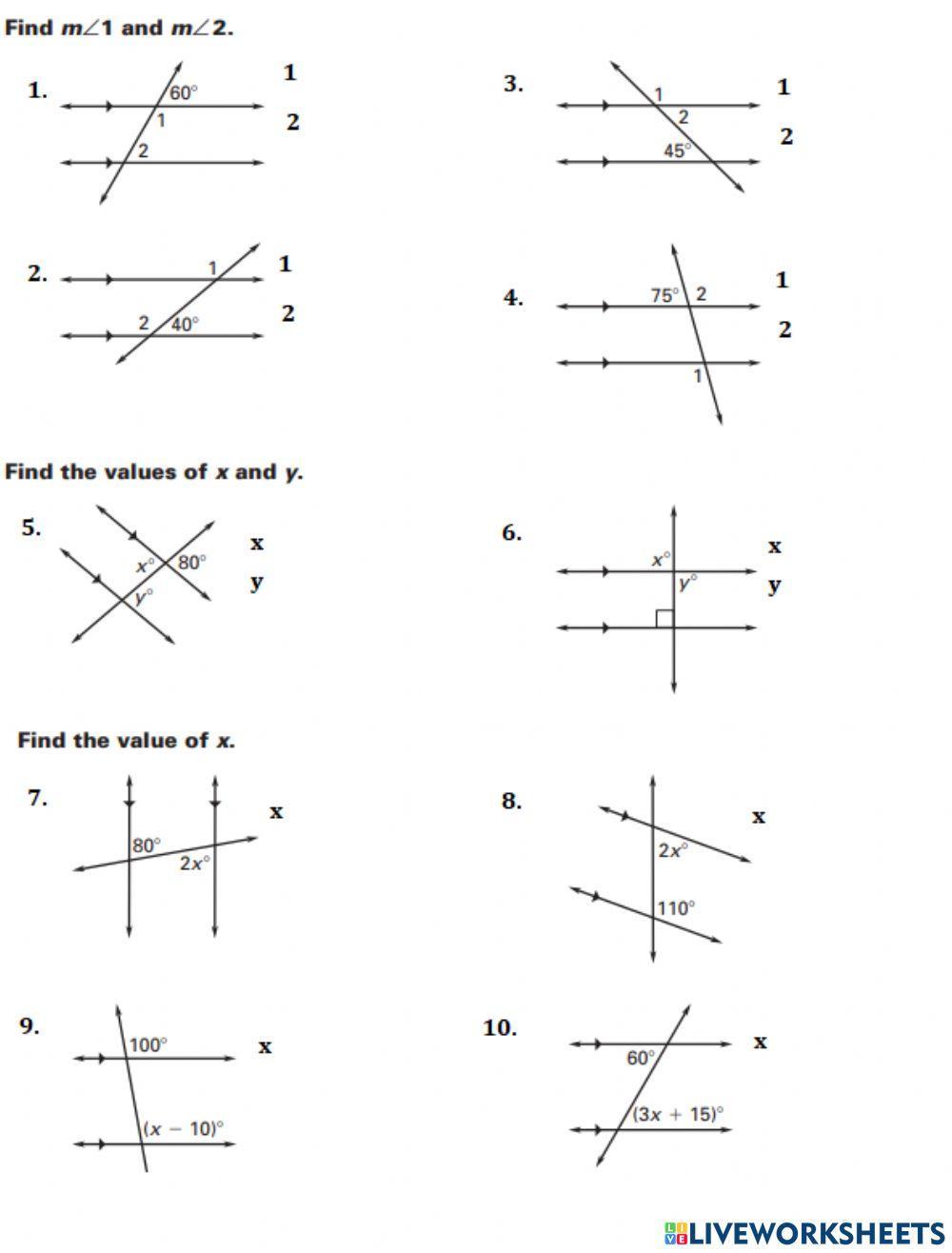
Understanding Parallel Lines and Transversals
Parallel lines and transversals are fundamental concepts in geometry, and understanding their properties is crucial for solving various mathematical problems. In this blog post, we will delve into the world of parallel lines and transversals, exploring their definitions, properties, and applications.
What are Parallel Lines?
Parallel lines are two or more lines that lie in the same plane and never intersect, no matter how far they are extended. In other words, parallel lines have the same slope and are always at the same distance from each other. The symbol “||” is used to denote parallel lines.
📝 Note: Parallel lines do not intersect, but they can be skew, meaning they are not coplanar.
What is a Transversal?
A transversal is a line that intersects two or more other lines, called the transversed lines. When a transversal intersects two parallel lines, it creates a pair of congruent angles, known as corresponding angles.
Properties of Parallel Lines and Transversals
When a transversal intersects two parallel lines, several important properties are observed:
- Corresponding Angles: The angles formed by the transversal and the parallel lines are congruent.
- Alternate Interior Angles: The angles formed by the transversal and the parallel lines on opposite sides of the transversal are congruent.
- Alternate Exterior Angles: The angles formed by the transversal and the parallel lines on the same side of the transversal are congruent.
- Interior Angles on the Same Side of the Transversal: The sum of the interior angles on the same side of the transversal is always 180°.
Types of Transversals
There are several types of transversals, including:
- Perpendicular Transversal: A transversal that intersects the parallel lines at a right angle (90°).
- Oblique Transversal: A transversal that intersects the parallel lines at an angle other than 90°.
Solving Problems with Parallel Lines and Transversals
Now that we have explored the properties of parallel lines and transversals, let’s apply this knowledge to solve some problems.
Example 1: Finding Corresponding Angles
In the diagram below, line AB is parallel to line CD, and line EF is a transversal. Find the measure of angle E.
 |
| Since line AB is parallel to line CD, corresponding angles are congruent. Therefore, angle E = angle G = 60°. |
Example 2: Finding Alternate Interior Angles
In the diagram below, line AB is parallel to line CD, and line EF is a transversal. Find the measure of angle F.
 |
| Since line AB is parallel to line CD, alternate interior angles are congruent. Therefore, angle F = angle H = 30°. |
📝 Note: Make sure to identify the corresponding and alternate angles correctly before solving problems.
In conclusion, parallel lines and transversals are essential concepts in geometry, and understanding their properties is vital for solving various mathematical problems. By applying the properties of corresponding angles, alternate interior angles, and alternate exterior angles, you can solve problems involving parallel lines and transversals with ease.
What is the symbol used to denote parallel lines?
+The symbol “||” is used to denote parallel lines.
What is the sum of interior angles on the same side of the transversal?
+The sum of interior angles on the same side of the transversal is always 180°.
What type of transversal intersects the parallel lines at a right angle?
+A perpendicular transversal intersects the parallel lines at a right angle (90°).
Related Terms:
- Teacher synergy llc
- Khan Academy
- IXL
- BrainPOP
- Udacity
- Duolingo



