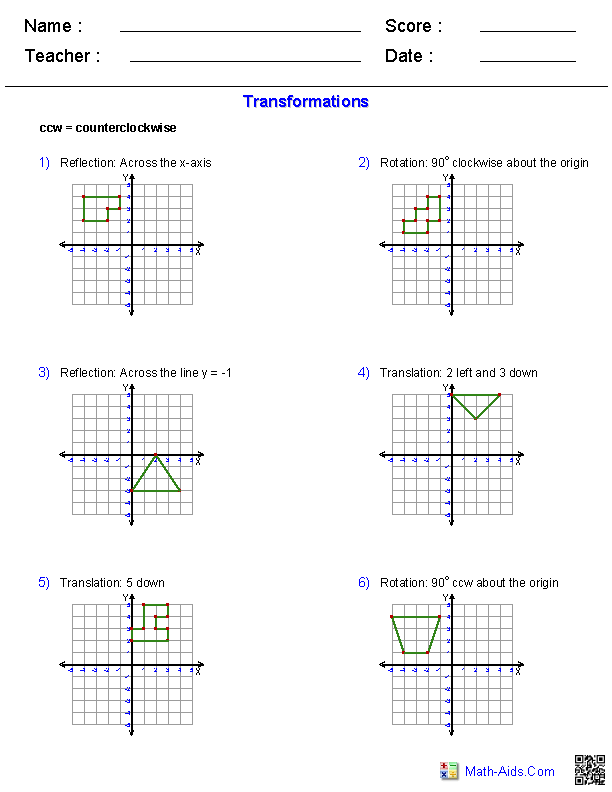
Exponents Worksheet: Practice Simplifying Expressions

Exponents Worksheet: Practice Simplifying Expressions

Are you ready to test your skills in simplifying expressions with exponents? This worksheet provides a comprehensive practice session to help you master the rules of exponents and apply them to various types of expressions.

Warm-Up Exercises

Before we dive into the more complex expressions, let’s start with some simple warm-up exercises to get you comfortable with the basics of exponents.

Simplify the following expressions:

• 2^3
• 5^2
• 3^4
• 2^5

Answers:

• 2^3 = 8
• 5^2 = 25
• 3^4 = 81
• 2^5 = 32

Product of Powers Rule

The product of powers rule states that when we multiply two powers with the same base, we can add the exponents.

Example:

• 2^3 × 2^4 =?

Solution:

• 2^3 × 2^4 = 2^(3+4) = 2^7

Practice Time!

Simplify the following expressions using the product of powers rule:

• 3^2 × 3^5
• 2^4 × 2^3
• 5^3 × 5^2

Answers:

• 3^2 × 3^5 = 3^(2+5) = 3^7
• 2^4 × 2^3 = 2^(4+3) = 2^7
• 5^3 × 5^2 = 5^(3+2) = 5^5

Power of a Power Rule

The power of a power rule states that when we raise a power to another power, we can multiply the exponents.

Example:

• (2^3)^4 =?

Solution:

• (2^3)^4 = 2^(3×4) = 2^12

Practice Time!

Simplify the following expressions using the power of a power rule:

• (3^2)^5
• (2^4)^3
• (5^3)^2

Answers:

• (3^2)^5 = 3^(2×5) = 3^10
• (2^4)^3 = 2^(4×3) = 2^12
• (5^3)^2 = 5^(3×2) = 5^6

Mixed Expressions

Now it’s time to practice simplifying mixed expressions that involve both multiplication and exponentiation.

Example:

• 2 × 2^3 × 3^2 =?

Solution:

• 2 × 2^3 × 3^2 = 2 × 8 × 9 = 144

Practice Time!

Simplify the following mixed expressions:

• 3 × 2^2 × 5^3
• 2 × 3^4 × 2^2
• 5 × 3^2 × 2^3

Answers:

• 3 × 2^2 × 5^3 = 3 × 4 × 125 = 1500
• 2 × 3^4 × 2^2 = 2 × 81 × 4 = 648
• 5 × 3^2 × 2^3 = 5 × 9 × 8 = 360

Challenge Time!

Are you ready for a challenge? Simplify the following complex expressions:

• (2^3 × 3^2)^4
• (5^2 × 2^3)^3
• (3^4 × 2^2)^2

Answers:

• (2^3 × 3^2)^4 = 2^(3×4) × 3^(2×4) = 2^12 × 3^8
• (5^2 × 2^3)^3 = 5^(2×3) × 2^(3×3) = 5^6 × 2^9
• (3^4 × 2^2)^2 = 3^(4×2) × 2^(2×2) = 3^8 × 2^4

📝 Note: Remember to follow the order of operations (PEMDAS) when simplifying complex expressions.

Now, take a deep breath and review your work. You’ve made it through the practice session! Keep practicing, and soon you’ll be a master of simplifying expressions with exponents.

Related Terms:

• Exponents worksheets PDF with answers
• Powers of 10 worksheet
• Exponent worksheet grade 8
• Homeschoolmath worksheets
• Worksheet math grade 6
• Exponent pdf