5 Ways to Master Domain and Range Worksheets
Understanding Domain and Range: A Fundamental Concept in Mathematics
When it comes to mathematics, particularly algebra and functions, understanding the concepts of domain and range is crucial. Domain and range worksheets are an essential tool for students to grasp these concepts and apply them to real-world problems. In this article, we will explore five ways to master domain and range worksheets, providing you with a comprehensive understanding of these fundamental concepts.
What is Domain and Range?
Before we dive into the ways to master domain and range worksheets, let’s first define what domain and range mean.
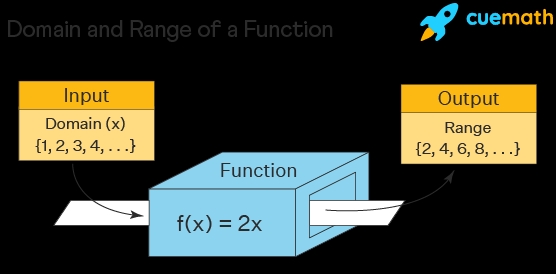
- Domain: The domain of a function is the set of all possible input values (x) that the function can accept. It’s the set of values that the function is defined for.
- Range: The range of a function is the set of all possible output values (y) that the function can produce. It’s the set of values that the function can return.
1. Understanding the Basics of Domain and Range
To master domain and range worksheets, you need to understand the basics of these concepts. Start by learning the definitions and formulas for domain and range. Practice identifying the domain and range of simple functions, such as linear and quadratic functions.
Tips:
- Always identify the type of function you’re dealing with (e.g., linear, quadratic, polynomial).
- Use the function’s equation to determine its domain and range.
- Graph the function to visualize its domain and range.
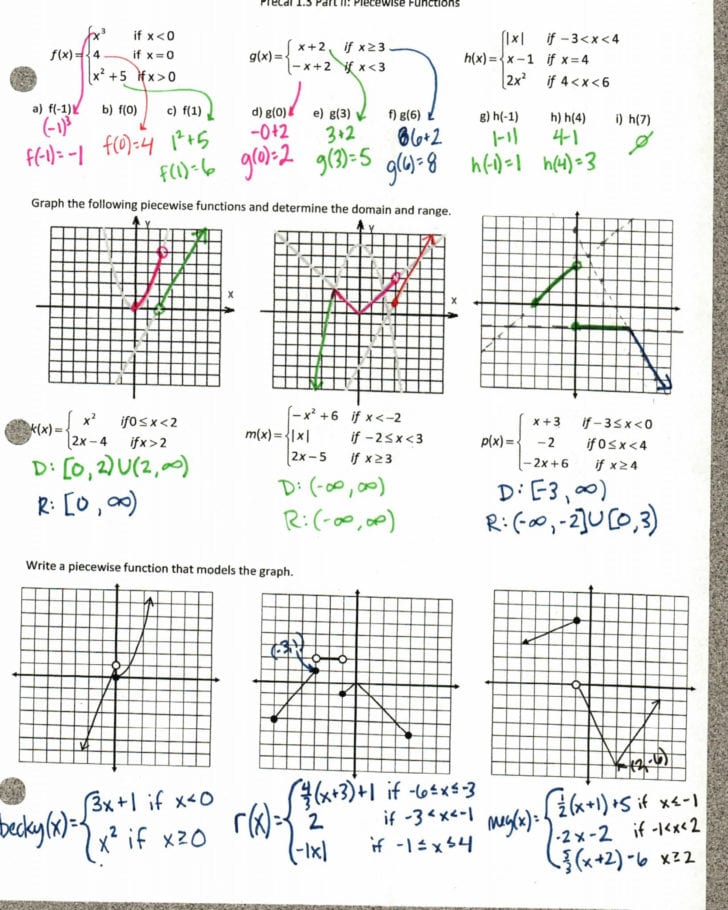
2. Identifying Domain and Range from Graphs
Graphs are an excellent way to visualize the domain and range of a function. By analyzing the graph, you can identify the domain and range of the function. Here are some tips:
- Domain: Look for the x-values that the function is defined for. These are the values on the x-axis where the graph exists.
- Range: Look for the y-values that the function produces. These are the values on the y-axis where the graph exists.
Example:
Suppose we have a graph of a quadratic function. The graph shows that the function is defined for x-values between -2 and 4, and the function produces y-values between -1 and 3. Therefore, the domain is [-2, 4], and the range is [-1, 3].
3. Using Algebraic Methods to Find Domain and Range
Algebraic methods involve using mathematical equations to find the domain and range of a function. Here are some tips:
- Domain: Use the function’s equation to identify any restrictions on the domain. For example, if the function has a denominator, the domain cannot include values that make the denominator equal to zero.
- Range: Use the function’s equation to identify any restrictions on the range. For example, if the function has a square root, the range cannot include negative values.
Example:
Suppose we have a rational function f(x) = 1/x. To find the domain, we need to identify any restrictions on the denominator. Since the denominator cannot be equal to zero, the domain is all real numbers except x = 0. To find the range, we can see that the function produces all real numbers except y = 0.
4. Practicing with Domain and Range Worksheets
Practice is key to mastering domain and range worksheets. Start with simple worksheets and gradually move on to more complex ones. Here are some tips:
- Start with simple functions: Begin with linear and quadratic functions and gradually move on to more complex functions.
- Use online resources: There are many online resources available that provide domain and range worksheets with answers.
- Check your work: Always check your work by graphing the function or using algebraic methods to verify your answers.
5. Applying Domain and Range to Real-World Problems
Domain and range have many real-world applications, such as physics, engineering, and economics. By applying domain and range to real-world problems, you can develop a deeper understanding of these concepts. Here are some tips:
- Read the problem carefully: Read the problem carefully and identify the function and its domain and range.
- Use the function’s equation: Use the function’s equation to identify any restrictions on the domain and range.
- Think critically: Think critically about the problem and use your knowledge of domain and range to solve it.
💡 Note: When solving real-world problems, it's essential to consider the context and any restrictions on the domain and range.
| Function | Domain | Range |
|---|---|---|
| f(x) = x^2 | All real numbers | All non-negative real numbers |
| f(x) = 1/x | All real numbers except x = 0 | All real numbers except y = 0 |
| f(x) = x^3 | All real numbers | All real numbers |
In conclusion, mastering domain and range worksheets requires a deep understanding of these fundamental concepts. By following these five ways, you can develop a comprehensive understanding of domain and range and apply them to real-world problems.
What is the difference between domain and range?
+The domain is the set of all possible input values (x) that a function can accept, while the range is the set of all possible output values (y) that a function can produce.
How do I find the domain and range of a function?
+You can find the domain and range of a function by using algebraic methods, graphing the function, or identifying restrictions on the domain and range.
What are some real-world applications of domain and range?
+Domain and range have many real-world applications, such as physics, engineering, and economics. They are used to model real-world problems and make predictions.
Related Terms:
- Domain and range Worksheet PDF
- Domain and Range Worksheet 1
- Domain and Range Worksheet 2
- Kuta domain and range Worksheet