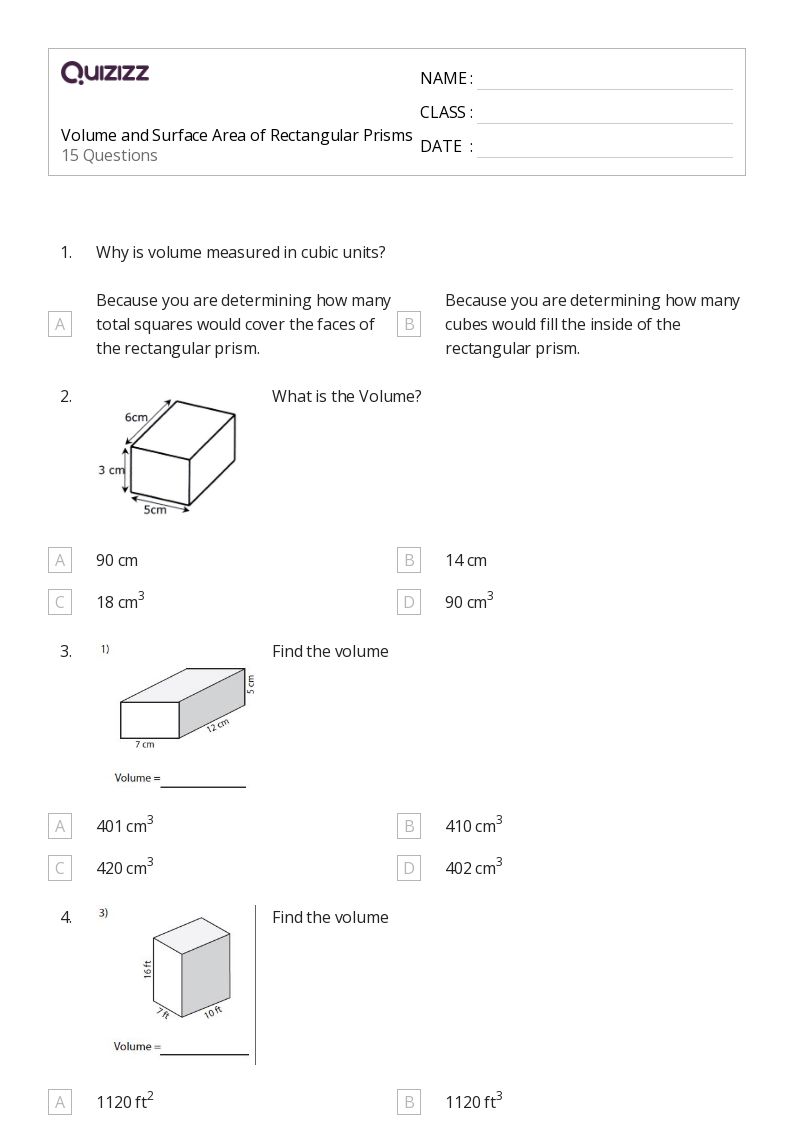
Volume of Prisms Worksheet: Practice Made Easy

Understanding the Concept of Volume of Prisms

When it comes to geometry, one of the fundamental concepts that students need to grasp is the volume of prisms. A prism is a three-dimensional solid object with two identical faces that are parallel and oriented in the same direction. The volume of a prism is the amount of space inside the prism, and it is measured in cubic units.

What is the Volume of a Prism?

The volume of a prism is calculated by multiplying the area of the base by the height. The formula for the volume of a prism is:

V = B × h

Where:

• V is the volume of the prism
• B is the area of the base
• h is the height of the prism

Types of Prisms

There are several types of prisms, including:

• Rectangular Prism: A prism with a rectangular base and four rectangular faces.
• Triangular Prism: A prism with a triangular base and three rectangular faces.
• Pentagonal Prism: A prism with a pentagonal base and five rectangular faces.

Calculating the Volume of a Prism

To calculate the volume of a prism, you need to know the area of the base and the height. Here are the steps:

1. Find the area of the base by multiplying the length and width of the base.
2. Multiply the area of the base by the height to get the volume.

Example 1: Rectangular Prism

Find the volume of a rectangular prism with a base area of 12 square cm and a height of 8 cm.

Solution

V = B × h V = 12 × 8 V = 96 cubic cm

Example 2: Triangular Prism

Find the volume of a triangular prism with a base area of 20 square cm and a height of 5 cm.

Solution

V = B × h V = 20 × 5 V = 100 cubic cm

Practice Problems

Now it’s your turn to practice calculating the volume of prisms. Here are some practice problems:

• Find the volume of a rectangular prism with a base area of 15 square cm and a height of 6 cm.
• Find the volume of a triangular prism with a base area of 25 square cm and a height of 4 cm.
• Find the volume of a pentagonal prism with a base area of 30 square cm and a height of 7 cm.

Answers

• 15 × 6 = 90 cubic cm
• 25 × 4 = 100 cubic cm
• 30 × 7 = 210 cubic cm

📝 Note: Make sure to label your answers with the correct units, which is cubic cm or cubic meters.

Tips and Tricks

• Make sure to understand the formula for the volume of a prism and how to apply it to different types of prisms.
• Practice, practice, practice! The more you practice calculating the volume of prisms, the more comfortable you will become with the concept.
• Use visual aids such as diagrams and drawings to help you understand the concept of volume.

Common Mistakes

• Forgetting to label the answers with the correct units.
• Confusing the formula for the volume of a prism with other formulas.
• Not understanding the concept of base area and height.

Conclusion

Calculating the volume of prisms is an important concept in geometry that requires understanding of the formula and practice. By following the steps outlined in this worksheet and practicing with different types of prisms, you will become more comfortable and confident in your ability to calculate the volume of prisms.