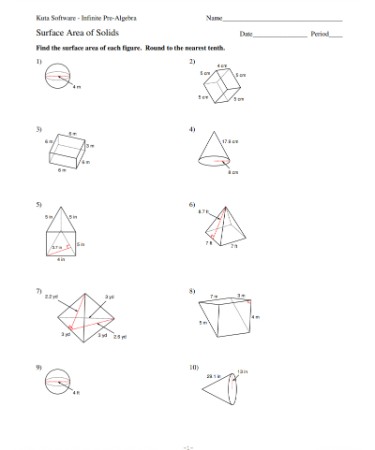
Triangle Sum Theorem Worksheet Practice
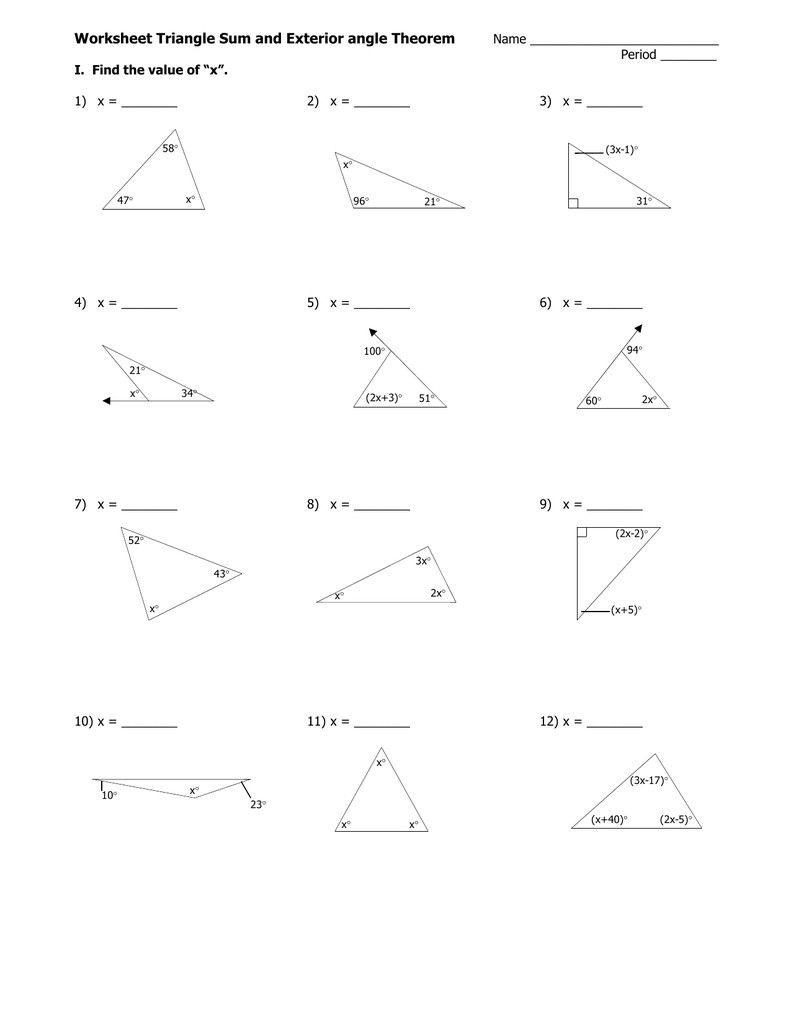
Triangle Sum Theorem: A Comprehensive Guide with Practice
The triangle sum theorem is a fundamental concept in geometry, stating that the sum of the interior angles of a triangle is always 180 degrees. This theorem has numerous applications in various fields, including mathematics, physics, and engineering. In this article, we will delve into the world of triangle sum theorem, exploring its definition, proof, and practical applications.
What is the Triangle Sum Theorem?
The triangle sum theorem states that the sum of the interior angles of a triangle is always equal to 180 degrees. Mathematically, this can be expressed as:
∠A + ∠B + ∠C = 180°
where ∠A, ∠B, and ∠C are the interior angles of the triangle.
Proof of the Triangle Sum Theorem
There are several ways to prove the triangle sum theorem. One of the most common proofs involves using parallel lines and transversals.
- Draw a triangle ABC.
- Draw a line parallel to side BC, passing through point A.
- Label the angles formed by the transversal as ∠1, ∠2, and ∠3.
Using the properties of parallel lines and transversals, we can show that:
∠1 + ∠2 + ∠3 = 180°
Since ∠1, ∠2, and ∠3 are corresponding angles to ∠A, ∠B, and ∠C, respectively, we can conclude that:
∠A + ∠B + ∠C = 180°
Practical Applications of the Triangle Sum Theorem
The triangle sum theorem has numerous practical applications in various fields, including:
- Geometry: The theorem is used to find missing angles in triangles, which is essential in solving geometric problems.
- Trigonometry: The theorem is used to derive trigonometric identities and formulas.
- Physics: The theorem is used to describe the motion of objects in two-dimensional space.
- Engineering: The theorem is used in the design of buildings, bridges, and other structures.
Triangle Sum Theorem Worksheet Practice
Now that we have explored the triangle sum theorem, it’s time to put our knowledge into practice. Here are some worksheet exercises to help you reinforce your understanding of the theorem:
Exercise 1: Finding Missing Angles
Find the measure of the missing angle in each triangle:
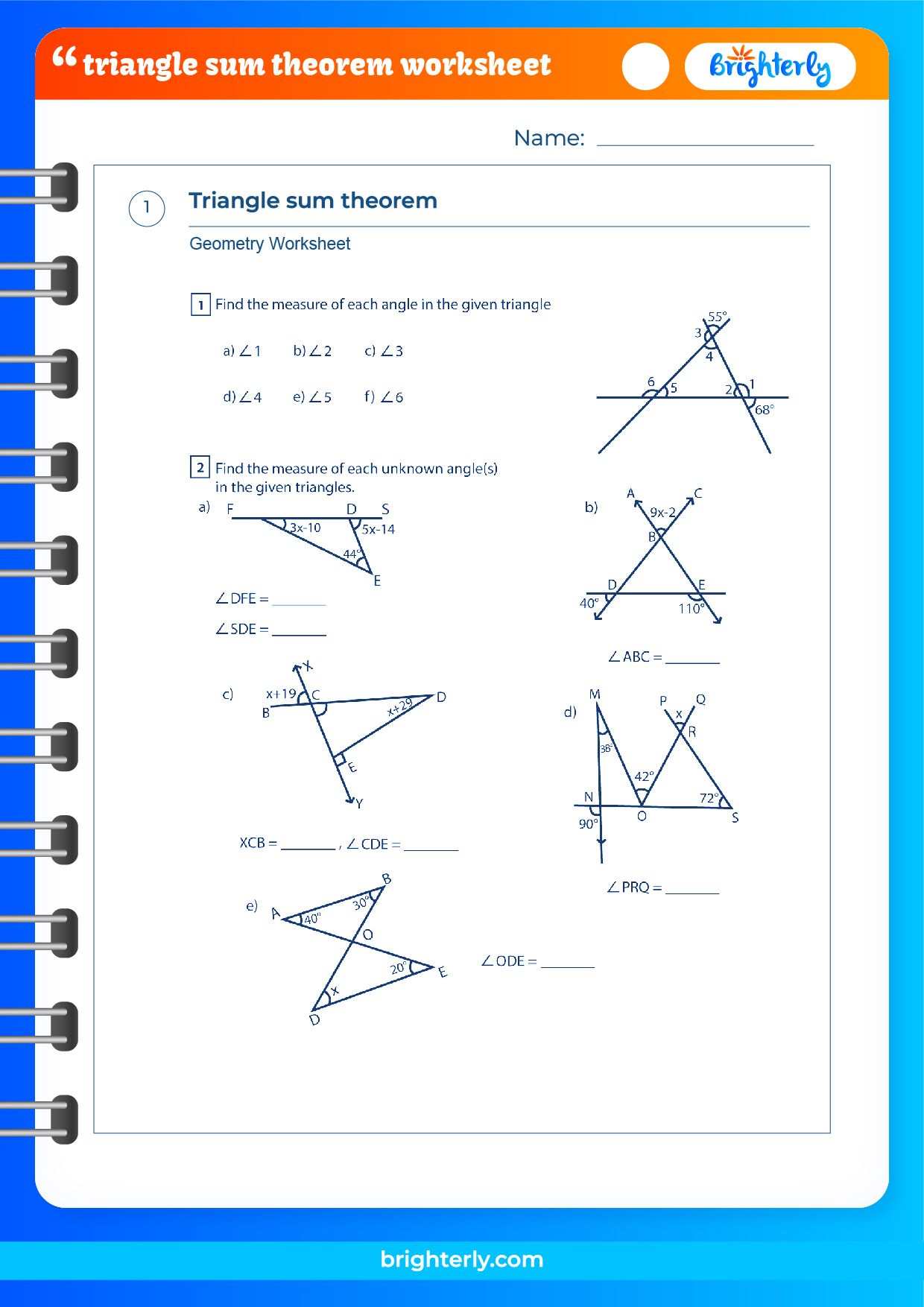
| Triangle | ∠A | ∠B | ∠C |
|---|---|---|---|
| ΔABC | 30° | 60° | ? |
| ΔDEF | 45° | 90° | ? |
| ΔGHI | 20° | 80° | ? |
Exercise 2: Proving the Theorem
Prove the triangle sum theorem using the parallel lines and transversals method.
Exercise 3: Real-World Applications
A surveyor is measuring the angles of a triangular field. If the measure of two angles is 60° and 80°, what is the measure of the third angle?
Notes
🔍 Note: The triangle sum theorem only applies to triangles with three sides. If a triangle has more than three sides, the theorem does not hold true.
Conclusion
In this article, we have explored the triangle sum theorem, its definition, proof, and practical applications. We have also provided worksheet exercises to help you reinforce your understanding of the theorem. Remember, the triangle sum theorem is a fundamental concept in geometry, and mastering it will help you solve a wide range of geometric problems.
What is the triangle sum theorem?
+The triangle sum theorem states that the sum of the interior angles of a triangle is always equal to 180 degrees.
How do you prove the triangle sum theorem?
+One way to prove the theorem is by using parallel lines and transversals.
What are some practical applications of the triangle sum theorem?
+The theorem has numerous applications in geometry, trigonometry, physics, and engineering.